Une suite numérique est une application (Un) définie de N→R par :
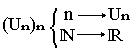
Convergence d'une suite
On dit qu'une suite (Un)b est convergente et converge vers L (L inférieur à l'infini),
![]()
La suite est dite divergente si:
![]()
Dès que
![]()
Opération sur les suites
On va supposer ci-après que deux suites (Un)n et (Vn)n convergentes respectivement vers L et M.
Conséquences
Somme
La suite (Un+Vn)n converge vers L+M.
Produit
La suite (Un.Vn) converge vers LM.
Différence
La suite (Un-Vn) converge vers L-M.
Quotient (avec M différent de 0)
La suite (Un/vn)n converge vers L/M
Proposition
Si une suite admet une limite L (L inférieur à l'infinie) alors celle-ci est unique.
Exemple
Soit la suite (Un)n de terme général Un=(-1)n
- Déterminer les limites respectives des deux sous suites (a2N)n et (b2N+1)n
a2N = U2N
b2N+1 = U2N+1 - Quelle est la limite de la suite (Un)n ?
Sens de variation
Sens de variation
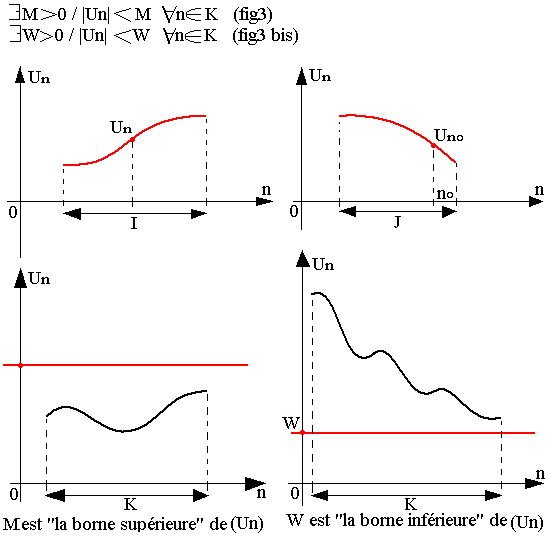
- Une suite Un est croissante sur un intervalle I si Un+1-Un est inférieure ou égale à 0 quelque soit n appartenant à I (fig1) ou encore Un+1/Un est supérieure ou égale à 1 quelque soit n appartenant à I.
- Une suite Vn est décroissante sur un intervalle J si Vn+1-Vn est inférieure ou égale à 0 quelque soit n appartenant à J (fig2) ou encore Vn+1/Vn inférieur ou égale à 1 quelque soit n appartenant à J
Borne d'une suite
On dit qu'une suite (Un)n est basée sur un intervalle K si:
Exercice 1:
Donnez la nature des suites ci-après:
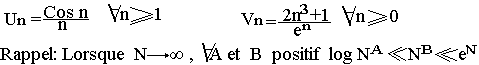
Suites arithmétiques / Suites géométriques
Suites arithmétiques
Suite U0, U1, U2 ... Un telle que quelque soit k appartenant à R Un=U0+nk quelque soit n supérieur ou égale à 0
Un = Un-1 + k
k : est la raison de la suite.
U0 : est son premier terme.
Somme partielle (SP)
Soit Sp = U0 + U1 + U2 + U3 + ... + Up-1
La somme de P premier termes de la suite (Un)n.
On montre que Sp = P/2[Up-1+U0]
Suites géométriques
C'est une suite V0, V
q est la raison de la suite
V0 est sont premier terme.
Somme partielle (SP)
Si Vp=V0+V1+V2+...+Vp-1, on montre que Sp=V0(1-qp)/(1-q)
Exercice:
La suite (Un)n définie par U0=0, U1=1, Un=7Un-1++8Un-2 quelque soit n supérieure à 2
Ecrire les 5 premier termes de cette suite.
Exercice:
On considère la suite gN définie par gN=UN+UN+1 écrire les 5 premiers termes de (GN)N
Montrez que (gN)N est une suite géométrique.
Convergences
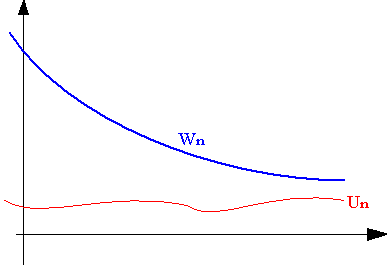
Soient (Un)n, (Vn)n et (Wn)n 3 suites numériques, vérifiant quel soit n appartenant à N Vn<Un<Wn
Convergence forcée
Si pour tout entier n, la suite (Wn)n est convergente, alors la suite (Un)n est convergente.
Divergence forcée
Si pour tout entier n, la suite (Vn)n est divergente alors la suite (Wn)n est divergente.
![]()
Exercice:
Etudions la nature des suites (Un)n et (Vn)n de terme généraux:
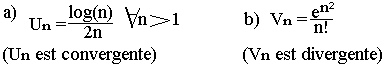
Exercice:
- Ecrire le terme général de la suite (Wn)n
-1; 4; 9; 16; -25; 36; 49; 64; -81; 100; ... - Soit la suite (Wn) de terme général
Wn = 1 + 1/n! + 1/2! + 1/3! + ... + 1/n! - Soit la suite de terme général an=Wn+1/n(n!)
Montrez que la suite (an)n est décroissante.
Convergences simples absolues
Toute suite croissante et majoré (respectivement décroissante et minorée) sur un intervalle I est convergent sur I.
Critère de Cauchy
Une suite est dite de "Cauchy" si:
![]()
Proposition:
Toute suite de Cauchy est convergente.
Exercice:
La suite de terme général Un=1-1/n est-elle une suite de Cauchy ?
Convergence absolue
Soit une suite alternée (prenant des valeurs positives et négatives)
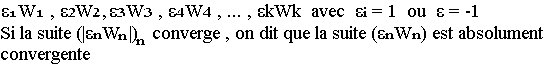
Exercice:
Soit (Vn)n une suite 1; -2/1!; 22/2!; -23/3!; 24/4!
- Donner le terme général de cette suite.
- Montrez que (Vn)n est absolument convergente.
Théorème de dérivation des séries de fonctions
Soient f0(x), f1(x), f2(x)... des fonctions définies et dérivables sur D, de dérivées respectives f'0(x), f'1(x), f'2(x)...

Théorème d'intégration des séries de fonctions
Soient g0(x), g1(x), g2(x), ... des fonctions définies et intégrable sur D, de primitive respectives sur [a,b]<D
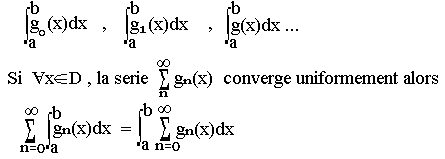
Application
Calculez la somme de la série fonction
-2x2 + 4x3 - 6x5 + 8x7 + ...
Résolution:
Un(x) = (-1)n2n(x)2n-1
Or Un(x) est la dérivée de Wn(x)
Si Wn(x)=(-1)nx2n
U1(x) + U2(x) + U3(x) + ... = W'1(x) + W2(x) + W3(x) + ...
Série entière
On appelle sertie entière une série de la forme
![]()
où x est une variable et les cœfficients ai ne dépendent pas de x (1) peut aussi s'écrire sur la forme
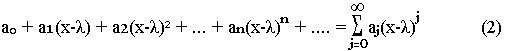
Rayon de convergence
On démontre que pour toute série entière il existe un nombre R(R>0) fini ou infini tel que la série est:
- Convergente si |x|<R
- Divergente si |x|>R
Le calcul d'un rayon de convergence d'une série entière se fait à partir des critères de convergence vu en cours.
Exemple:
Par le critère de d'Alembert, on a:
![]()
