Les applications
Une application est une relation définie entre des éléments d'un ensemble de départ et d'un ensemble d'arrivée. Chaque élément de l'ensemble de départ admet une image et une seule dans l'ensemble d'arrivée (fig1)
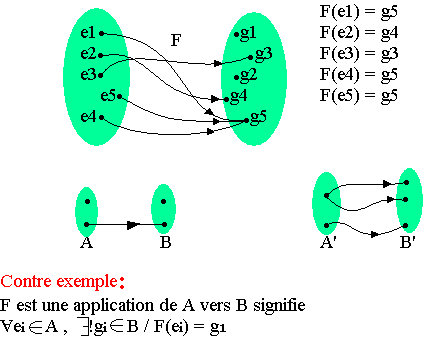
Nombre d'application entre deux exemples
On peut dénombrer le nombre d’application possible entre un ensemble de départ E à P élément s et un ensemble d'arrivée F à k éléments. Ce nombre est n=kp
Applications injectives
Une application est dite injective ou "injection" lorsque chaque élément de l'ensemble d'arrivée est image d'au plus un seul élément de l'ensemble P de départ (fig2)
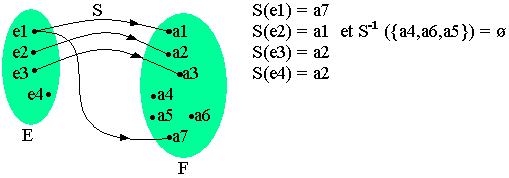
Remarque:
Pour injection d'un ensemble A vers un ensemble B on a card(B) supérieur ou égale à card(A).
Une application G de A→B est injective signifie
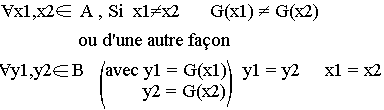
Nombre d'injection entre deux ensembles
On dénombre le nombre d'injection possible entre un ensemble de départ E (#E=P) et un ensemble d'arrivée F (#F=n). Ce nombre est:
![]()
Application surjectives
Au contraire de l'application injective qui ne tolère que 1 ou 0 antécédent, une application surjective ou "surjection" permet à tout élément de l'ensemble d'arrivée d'avoir un ou plusieurs antécédents dans l'ensemble de départ (fig3)
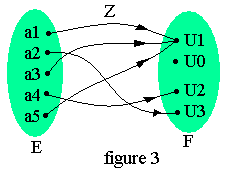
- Z n'est pas une surjection de E vers F
- Z est une surjection de E vers F-{U0}
Une application g de A vers B est surjective signifie
![]()
Remarque:
Si on a A une surjection de A→B alors card(A) est supérieur ou égale à card(B).
Applications bijectives
Une application bijective est à la fois une injection et une surjection.
Ainsi A est une bijection de E vers F signifie:
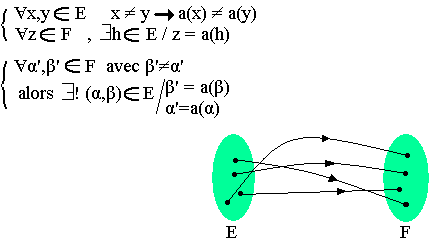
Pour une bijection de E vers F on a #E = #F
Nombre de bijection d'un ensemble
On peut dénombrer le nombre de bijection entre deux ensembles A et B (card(A)=card(B)=M), ce nombre est n=M!
Composition d'application / Application réciproque
Soit f et g deux application définies de A→B et de B→C respectivement (fig3)
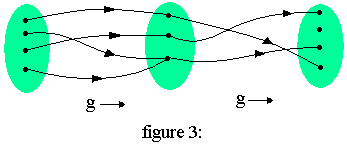
Alors on appelle composée de f par g l'application notée gof qui à tout élément xA de A associe un élément Z
Réciproque d'une application
Si f est une application de A→B quelque soit x appartenant à A, f(x) existe dans B.
f admet une réciproque f-1 de f(A)→A si et seulement si f est une injection de A→B auquel cas:
![]()
Inverse d'une composée
Si Z=gof alors la réciproque de Z est Z-1=(fog)-1=g-1of-1
