Fonctions

Une fonction est une relation ø d'un ensemble E vers un ensemble F telle que il existe une partie DCE pour laquelle la fonction de ø à D est une application de D vers øDCF.
D est appelé le domaine de la fonction de ø

Continuité d'une fonction réelle

Fonction continue

On dit que f est une fonction continue sur un support ACD_f si:

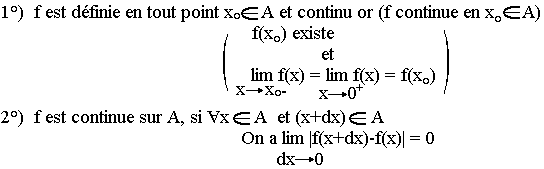
(1) et (2) sont équivalents.

Propriétés fondamentales

On va supposer pour la suite que f et g sont deux fonctions continues sur un support D
On a les propriétés suivantes:

Conséquence:

Si f est continue sur D, alors l'image d'un intervalle ouvert U. est un intervalle ouvert f(U).

Fonctions de classe C_N[a, b]

Soit f une fonction continue sur [a, b], alors si f admet une dérivée d'ordre N, f(N) continue sur [a,b], alors f est dite de classe C^N sur [a,b].

Non continuité / points de discontinuité

Lorsqu'une fonction g sur A présente dans sa représentation une famille F_R={x₁,x₂,...,x_k} de points de A tel que g(x) n'est pas définie, alors g est dite continue presque partout sur A lorsque g est continue sur A-F.

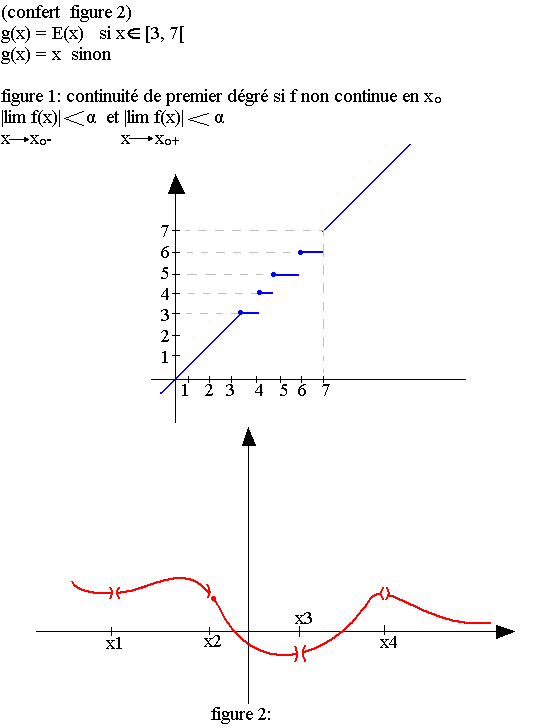
Continuité presque partout.
La fonction présente un nombre fini de discontinuité.

Parité et périodicité de fonctions

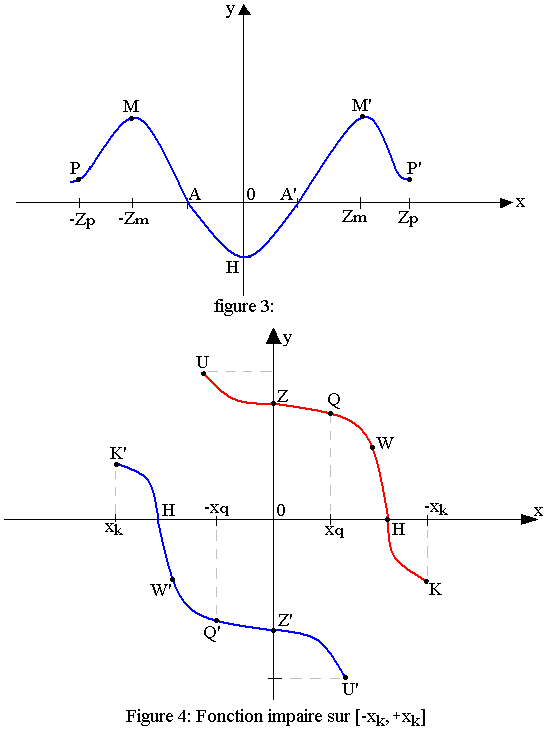
Fonctions paires

ƒ est une fonction paire sur D_f, si quelque soit x appartenant à D_f; f(x)=f(-x)
La courbe représentative de f est présentée alors une symétrie par rapport à l'axe oy.

Fonctions impaires

g est une fonction impaire sur D_g si quelque soit x appartenant à D_g; g(-x)=-g(x).
La courbe de g est symétrique par rapport à l'origine 0.