Les applications
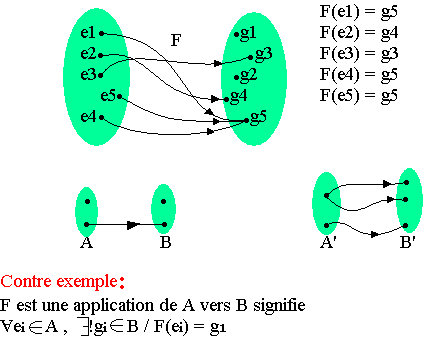
Une application est une relation définie entre des éléments d'un ensemble de départ et d'un ensemble d'arrivée. Chaque élément de l'ensemble de départ admet une image et une seule dans l'ensemble d'arrivée (fig1)
Nombre d'application entre deux exemples
On peut dénombrer le nombre d’application possible entre un ensemble de départ E à P élément s et un ensemble d'arrivée F à k éléments. Ce nombre est n=kp
Applications injectives
Une application est dite injective ou "injection" lorsque chaque élément de l'ensemble d'arrivée est image d'au plus un seul élément de l'ensemble P de départ (fig2)
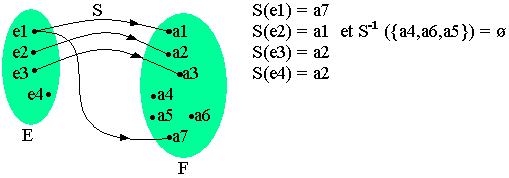
Remarque:
Pour injection d'un ensemble A vers un ensemble B on a card(B) supérieur ou égale à card(A).
Une application G de A→B est injective signifie
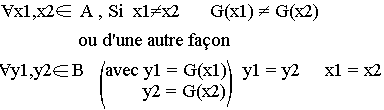
Nombre d'injection entre deux ensembles
On dénombre le nombre d'injection possible entre un ensemble de départ E (#E=P) et un ensemble d'arrivée F (#F=n). Ce nombre est:
![]()
Application surjectives
Au contraire de l'application injective qui ne tolère que 1 ou 0 antécédent, une application surjective ou "surjection" permet à tout élément de l'ensemble d'arrivée d'avoir un ou plusieurs antécédents dans l'ensemble de départ (fig3)
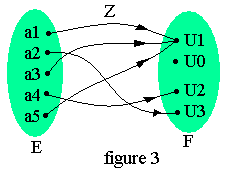
- Z n'est pas une surjection de E vers F
- Z est une surjection de E vers F-{U0}
Une application g de A vers B est surjective signifie
![]()
Remarque:
Si on a A une surjection de A→B alors card(A) est supérieur ou égale à card(B).
Applications bijectives
Une application bijective est à la fois une injection et une surjection.
Ainsi A est une bijection de E vers F signifie:
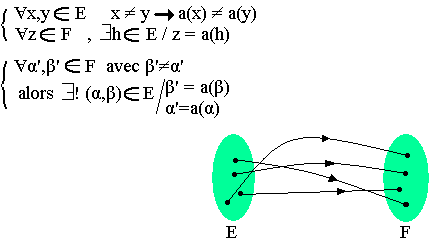
Pour une bijection de E vers F on a #E = #F
Nombre de bijection d'un ensemble
On peut dénombrer le nombre de bijection entre deux ensembles A et B (card(A)=card(B)=M), ce nombre est n=M!
Composition d'application / Application réciproque
Soit f et g deux application définies de A→B et de B→C respectivement (fig3)
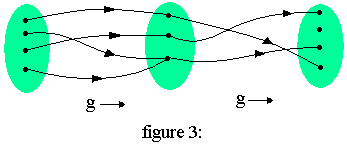
Alors on appelle composée de f par g l'application notée gof qui à tout élément xA de A associe un élément Z
Réciproque d'une application
Si f est une application de A→B quelque soit x appartenant à A, f(x) existe dans B.
f admet une réciproque f-1 de f(A)→A si et seulement si f est une injection de A→B auquel cas:
![]()
Inverse d'une composée
Si Z=gof alors la réciproque de Z est Z-1=(fog)-1=g-1of-1
Fonctions
Une fonction est une relation ø d'un ensemble E vers un ensemble F telle que il existe une partie DCE pour laquelle la fonction de ø à D est une application de D vers øDCF.
D est appelé le domaine de la fonction de ø
Continuité d'une fonction réelle
Fonction continue
On dit que f est une fonction continue sur un support ACDf si:
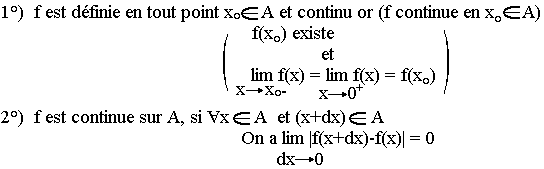
(1) et (2) sont équivalents.
Propriétés fondamentales
On va supposer pour la suite que f et g sont deux fonctions continues sur un support D
On a les propriétés suivantes:
- (f+g) est continue sur D
- (f*g) est continue sur D
- (f/g) est continue sur D en tout point x0, g(x0) différent de 0
- Su f continue sur D, alors fog est continue sur D.
- Si f est strictement monotone sur D alors sa réciproque f-1 est strictement monotone sur f(D)
Conséquence:
Si f est continue sur D, alors l'image d'un intervalle ouvert U. est un intervalle ouvert f(U).
Fonctions de classe CN[a, b]
Soit f une fonction continue sur [a, b], alors si f admet une dérivée d'ordre N, f(N) continue sur [a,b], alors f est dite de classe CN sur [a,b].
Non continuité / points de discontinuité
Lorsqu'une fonction g sur A présente dans sa représentation une famille FR={x1,x2,...,xk} de points de A tel que g(x) n'est pas définie, alors g est dite continue presque partout sur A lorsque g est continue sur A-F.
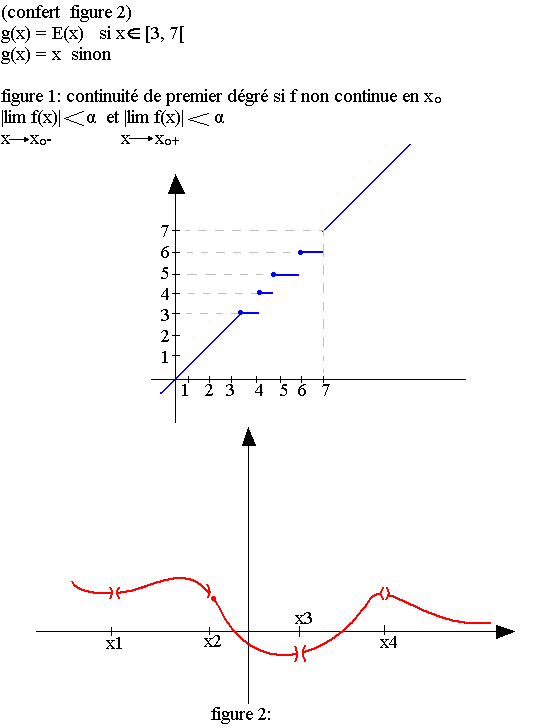
Continuité presque partout.
La fonction présente un nombre fini de discontinuité.
Parité et périodicité de fonctions
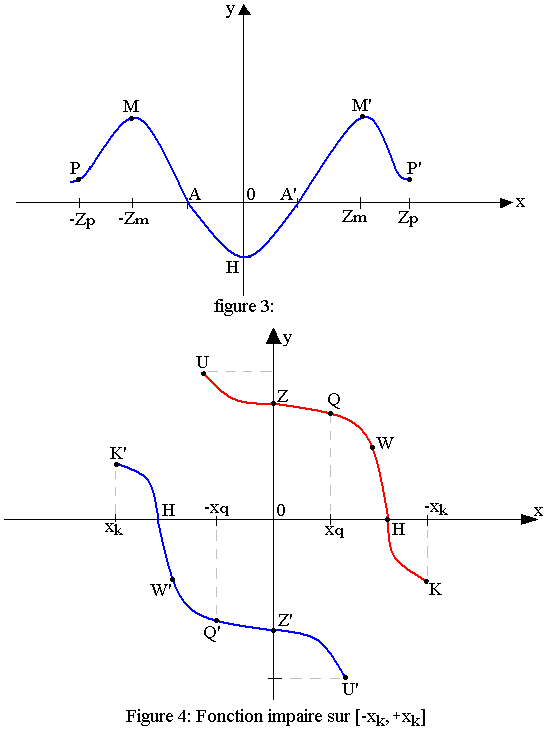
Fonctions paires
ƒ est une fonction paire sur Df, si quelque soit x appartenant à Df; f(x)=f(-x)
La courbe représentative de f est présentée alors une symétrie par rapport à l'axe oy.
Fonctions impaires
g est une fonction impaire sur Dg si quelque soit x appartenant à Dg; g(-x)=-g(x).
La courbe de g est symétrique par rapport à l'origine 0.