Développements limités
On dit qu'une fonction f, Cnn+1 de A vers R admet un développement limité d'ordre N au voisinage de x0 appartenant à A, noté DJn(x)(f). S'il existe un polynôme PN d'ordre inférieur ou égal à n et une fonction qui vérifient
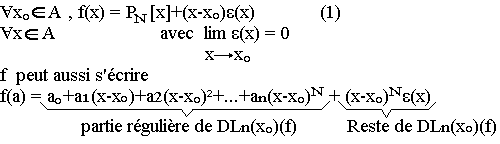
Existence et unité du DLn(x)f
Existence
Montrons qu'une fonction f de classe CN+1[a+b] peut s'écrire sous forme polynomiale: f(x)=a0+a1(x-x0)+a2(x-x0)2+...+an(x-x0)N+RN(x) où RN(x) est l'erreur d'approximation.
RN(x0)=0 on aura:
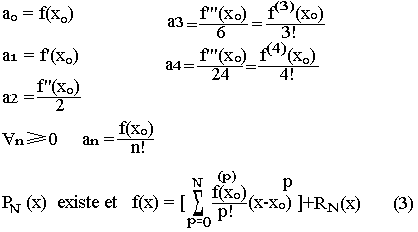
(3) est le polynôme de Taylor de f lorsque x0=0, c'est la formule de MacLaurin très utilisée dans les calculs de limites.
Unicité
Supposons que f admettent deux DLn(x0):
DLx1(x0)(f): Qn(x) + Rn(x) = q0 + q1(x-x0) + q2(x-x0)2 + ... + qn(x-x0)n + Rn(x) = f(x)
DLx2(x0)(f) : Zn(x) + Pn(x) = Z0 + Z1(x-x0) + Z2(x-x0) + ... + Zn(x-x0)n + Pn(x) = f(x)
En utilisant de proche en proche les dérivées successives f(N)(x0), on montre facilement que (q0=Z0; q1=Z1; q2=Z2; ...; qn=Zn) Rn=Qn.
Formule du reste Rn(x)
Si la partie régulière du DLn(x0)(ƒ) s'écrit:
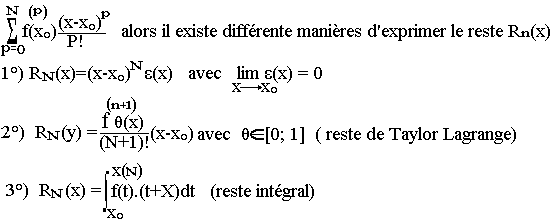
Exercice:
Déterminez le DL4(x0=0) : x → ex
Déterminez le DL2(x0=0) : x→ Cos(xe-x)
Déterminez le DL2(x →) : x→ ln(x+1)/Sh(x)
(Indication: Sh(x)=(ex-e-x)/2 )
Résolution:
f(x) = ex
f'(x) = ex
f"(x) = ex
f"'(x) = ex
fN(x) = ex
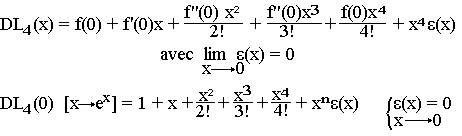
Ce DL4 permet d'étudier le comportement de x → ex au voisinage de 0
Développement en série entière d'une fonction
Soit f une fonction de classe C [a, b], on montre que si:
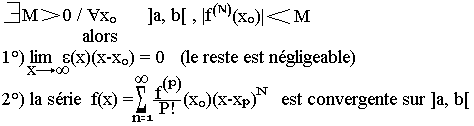
Opération sur les développements limités
Supposons deux fonctions f et g Ck[a,b] et x0 appartenant à ]a,b[
DLN(x0)(f+g) = DLN(x0)(f) + DLN(g)
DLN(x0)(f.g) = DLN(x0)(f).DLN(x0)(g)
DLN(x0)(f/g) = DLN(x0)(f)/DLN(x0)(g)
DLN(x0)(fog) = DLNf[DLN(x)g]
Application à l'étude des positions dans le plan
Soit f une fonction définie sur [a, b] et x0 appartenant à ]a, b[. On suppose que f est Ck[a,b] avec k supérieur ou égale à 2
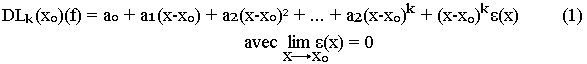
Position relative d la courbe de f: Cf
Supposons que T est la tangente à Cf au voisinage de x0, l'équation de T est yT=a0+a1(x-x0).
La position de Cf par rapport à T sera donnée par le terme de la partie régulière de (1)
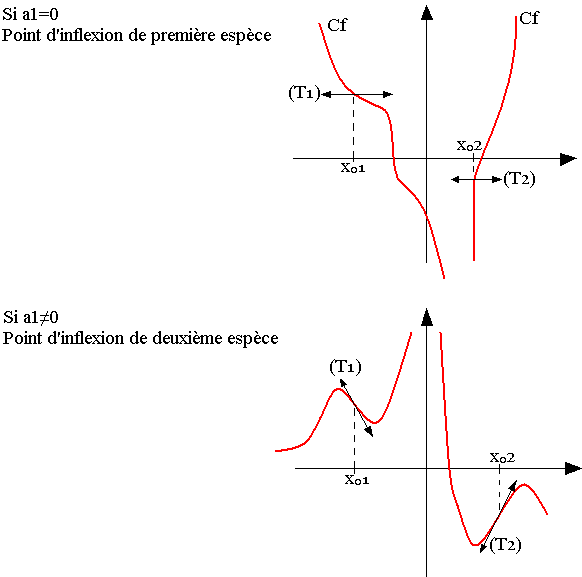
Si k est pair
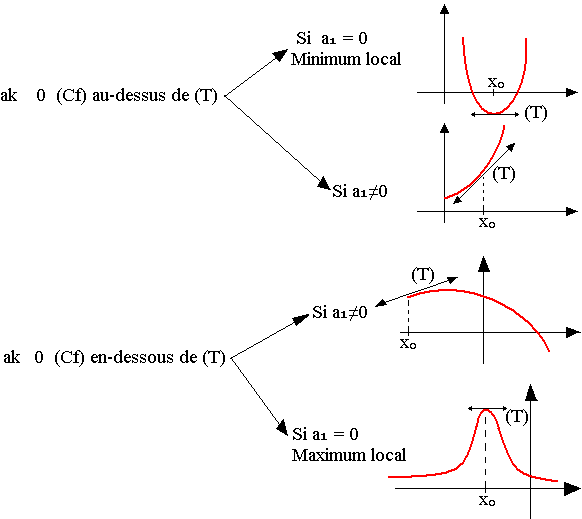
Si k est impair
Les positions de (Cf) par rapport à T varient avec le signe de ak(x-x0)k.
Exercice:
Montrez qu'on peut développer en série entière la fonction x→3x
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale