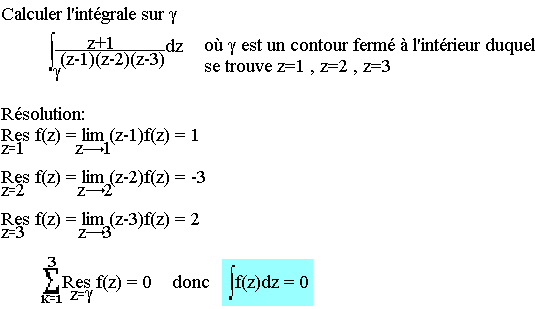Intégrales de fonctions complexes

Différentielle d'une fonction complexe

Soit f une fonction complexe de classe C¹ dans un voisinage de Z₀. Posons ƒ(z)=U(x,y)+iV(x,y) où u et v sont de classe C¹ dans un voisinage de (x₀,y₀).
Alors le développement limité à l'ordre 1 de ƒ(z) au voisinage de Z₀ est:

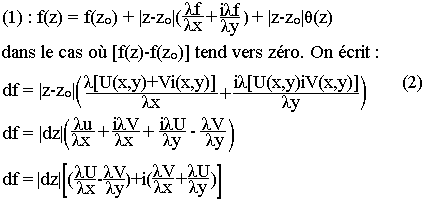
dƒ est différentielle si le deuxième facteur du deuxième membre tend vers zéro.

Intégration

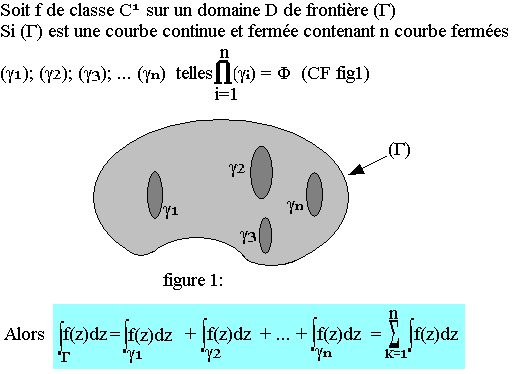
f étant de classe C' sur un domaine D, soit un arc de courbe alors:

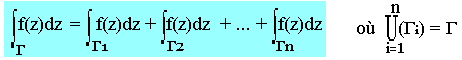
Propriétés

Propriété 1

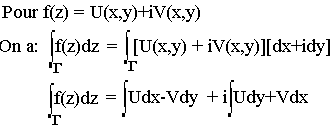
Propriété 2

Si Ø est une primitive de f au voisinage de Z₀ alors:

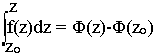
Propriété 3

Les résidus

Soit a un pôle d'ordre n d'une fonction ƒ(z) définie en série de Laurent.
On appelle résidus de ƒ(z) en a noté Resƒ(z); le réel:

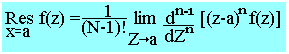
Ou encore, si ƒ(z)=N(z)/F(z) admet un pôle x=a d'ordre 1 alors Resf(z)=N(a)/D(a)

Théorème fondamentale

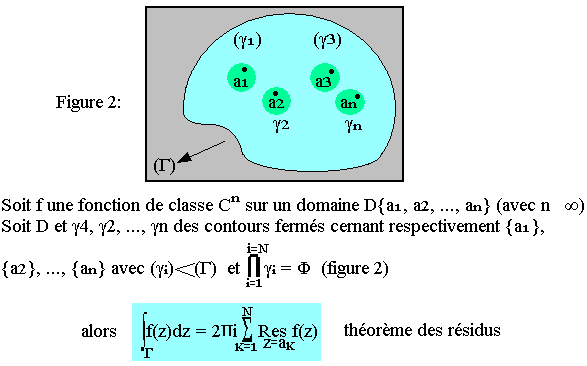
Applications