Transformée en Z
Signal échantillonné
Soit x(t) une fonction vérifiant les conditions de Dirichlet, l'échantillonnage de x(t) est la fonction (confer figure 1)
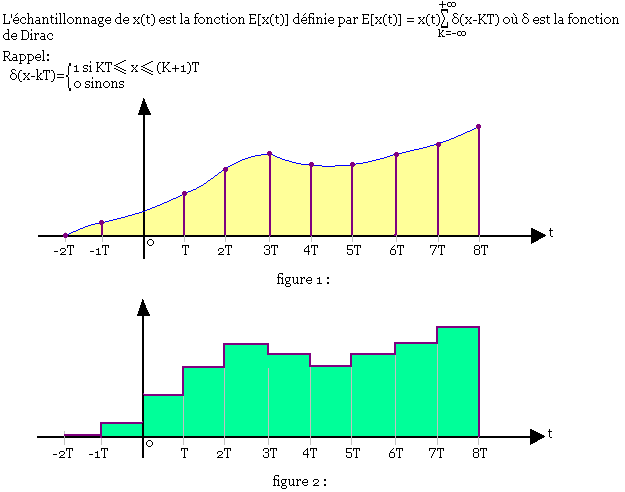
Nous allons supposer sur R tout entier et que l'intégrale de x(t)dt converge.
Désignons par L(f(t)) la transformée de Laplace de f(t) étendu sur ]-∞;+∞[
Définition
On distingue X(z) la transformée en z de x(t), alors:
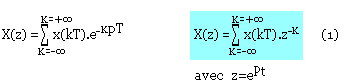
Définition
Si x(t)=0 lorsque t<0 alors X(z) est la transformée de la Laplace discrète de E[x(t)].
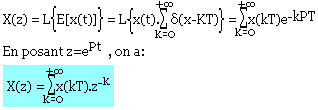
Exercice:
Déterminez la transformée en z des systèmes suivants.
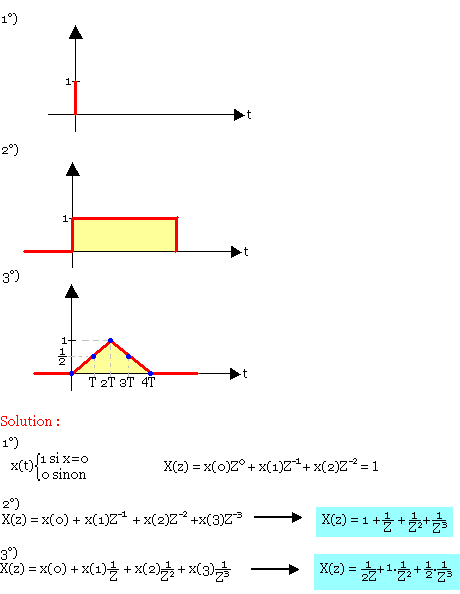
Transformée en Z inverse
La transformée inverse de X(z) obéit aux mêmes règles que la transformée de Laplace inverse. On utilise selon les cas, des règles de division des puissances ou du théorème de résidus.
Exemple
Si X(z) est polynôme en Z-N avec N inférieur à l' infini, l'inverse est immédiat.
Exemple:
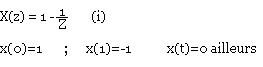
Si X(z) est une fraction en Z formule des résidus.
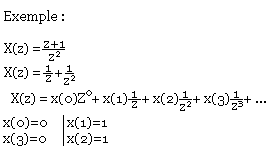
Exercices
- Déterminez X(z) qi x(t) est donné par la fonction en escalier (figure 1)
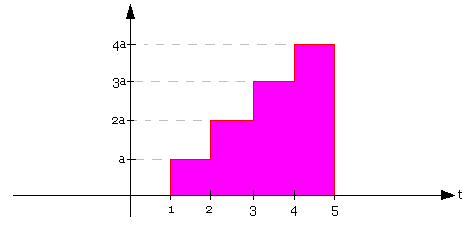
- Déterminez x1(t) si X(z) = (Z4-2Z2+1)/Z3
Transformée de Fourrier à cosinus (TFC) et à sinus (TFS)
Si f est une fonction transformable en série de Fourrier sur:
Transformée et parité de f
Si f est une fonction vérifiant la condition (C1) alors:
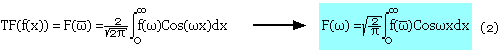
Si f vérifie (c1) et f impaire on aura:
Transformée en cosinus et en sinus
Les équations (2) et (3) précédents sont intéressantes, surtout lorsqu’il s'agit de convertir un signal temporel en un spectre fréquentiel. C'est pourquoi elles ont été utilisées même pour des fonctions ni paires ni impaires. On définit alors les transformée de Fourier en cosinus (TFC) et les transformées de Fourrier en sinus (TFS).
TFC/TFS
Si une fonction vérifie (c1) sur un intervalle [a, b], alors ses transformées en cosinus et en sinus existent et sont définies par:
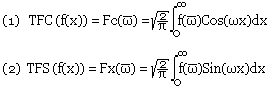
Exercice
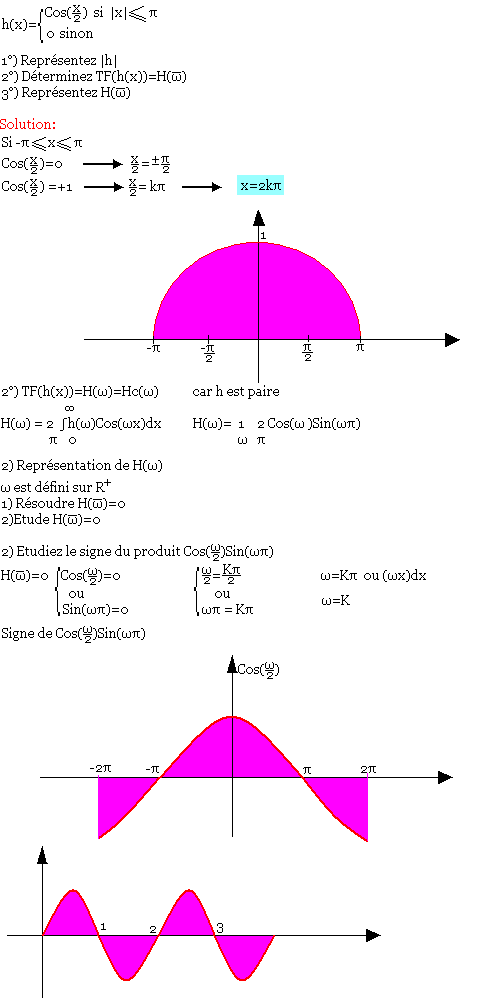
Soit la fonction h définie par:
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale