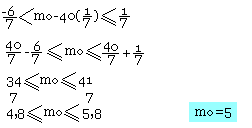Elément d'analyse combinatoire

Considérons un ensemble de n éléments différents, un échantillon aléatoire a₁, a₂, ... a_n de ces éléments seront appelés groupement.
Par exemple: Lorsqu'on jette une pièce de monnaie 10 fois, sa tombée du côté face (F) et du côté pille (P) peut donner le groupement suivant: FFFPPFPPP

Binôme de NEWTON

Loi binomiale : épreuve de BERNOUILLI

Si on effectue N épreuves indépendantes et si la probabilité de réalisation d'un événement A(succès) dans chacun de ces épreuves est invariable, égale à P. Alors la probabilité d'apparition n fois de l'événement A(en succès) dans ces m épreuves est donnée par la formule de BERNOULLI.

B_N[m,p] = P_N(m) = P(X=m)
C^m_NP^mq^N-m

Avec m: nombre de succès
P: probabilité de succès
N: nombre d'épreuve.
q=1-p est la probabilité d'un échec.

Exercice:

Une urne contient 30 boules: 20 blanches et 10 noires: L'expérience est la suivante:
On tire 4 boules suite (avec remise et brassage)

Résolution:

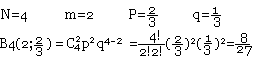
1. Soit A_i l'événement "obtenir i boules blanches en 4 épreuves"
   Soit E l'événement "obtenir au moins 1 boule blanche en 4 épreuves"
   Prob(E) = Prob(A₁)+Prob(A₂)+Prob(A₃)+Prob(A₄)
   Prob(A₁) = C¹₄p¹q³ = (4)(2/3)¹(1/3)³
   Prob(A₂) = C²₄p²q² = (6)(2/3)²(1/3)³(1/3)²
   Prob(A₃) = C³₄p³q¹ = (4)(2/3)³(1/3)¹
   Prob(A₄) = C⁴₄P⁴
   Prob(E) = 8/81 + 24/81 + 32/81 + 16/81 = 80/81
   
   Autre méthode:
   E (contraire de E) "Obtenir 0 boule en 4 épreuves"
   P(E) = 1 - P(E)
   P(E) = 1 - P(E)
   Calculons P(E_U) = 1 - P(E)
   P(E) = 1 - P(E)
   Calculons P(E) = B₄(0;2/3) = C⁰₄p⁰q⁴
   P(E) = (1)(1/3)⁴ = 1/81
   P(E) = 1 - 1/81
   P(E) = 80/81

Quel est le nombre d'apparition de la boule blanche dans une épreuve?

Nombre le plus favorisé

On définit le nombre le plus favorisé m₀ d'apparition d'un "succès" au bout de N épreuves. Ce nombre m vérifie

A la suite des observations entreprises pendant une période de temps prolongée, on a constaté que la probabilité que la pluie tombe dans une certaine ville est de 1/7.
Déterminez le nombre le plus favorisé le jour pluvieux le premier Octobre dans la ville donnée au cours de 40ans.
N=40 ; p=1/7 ; q=1-1/7=6/7
Résolution: