Les droites - Droites perpendiculaires

Droites perpendiculaires

Deux droites sont perpendiculaires lorsqu’elles se coupent en un point en formant des angles droits.
Construction:

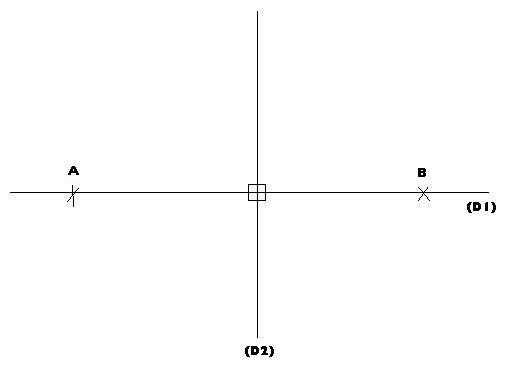
Les droites (D1) et (D2) sont perpendiculaires.

Deux droites perpendiculaires sont sécantes.
On peut ainsi à l'aide d'une règle et d'une équerre tracez plusieurs droites perpendiculaires à une seule.

Exemple:

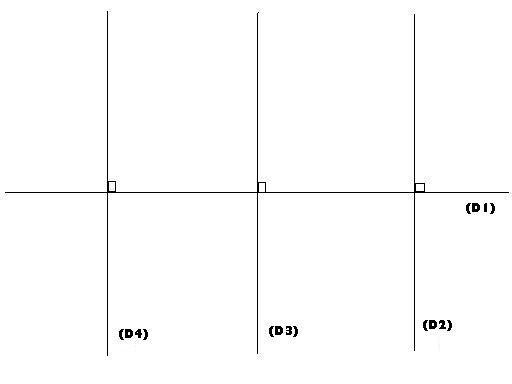
(D2), (D3) et (D4) sont perpendiculaires à (D1)

Définition:

Deux droites sont parallèles lorsqu'elles ne se rencontre jamais ou encore lorsqu'elles n'ont aucun point commun.

(D1) et (D2) sont parallèles. On note (D1)//(D2)

Activité:

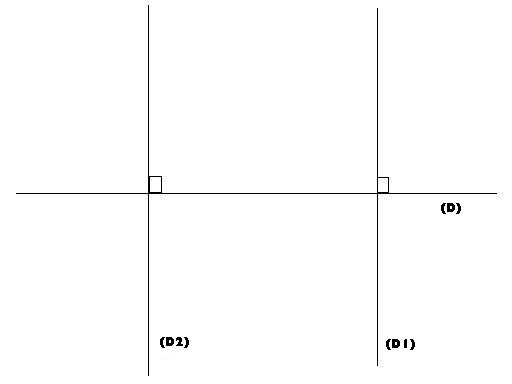
Soit (D1) et (D2), deux droites perpendiculaires à une droite (D). Que peut-on dire

On peut dire que (D1)//(D2)

Définition:

Deux droites perpendiculaires à une même droite sont parallèles. De même deux droites parallèles à une même droite, sont parallèles.

Soient (D1) et (D2)//(D1). Si (D1)//(D2) deux droites parallèles, si la droite (D) est perpendiculaire à (D1) elle l'est aussi à (D2).

Demi droites segments: Demi-droites:
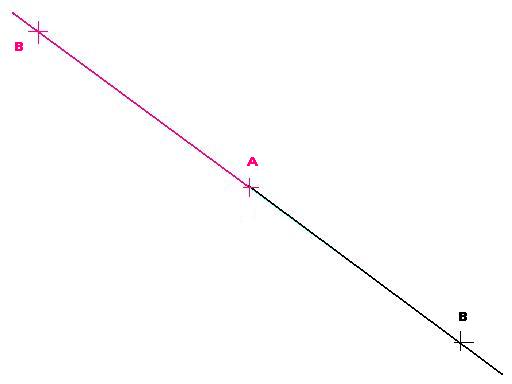
Tracez une droite (D), placez les points A, B et R contenant le point B seulement.

Solution:

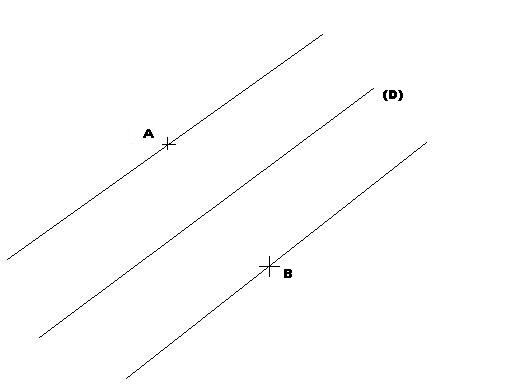
La partie rouge de la droite (D) sur la figure est une demi-droite. Cette demi-droite a pour origine le point A et passé par le point B. Cette demi-droite est illimitée du côté du point B. Elle s'écrit ou se note (AB). On dit que la droite est le support de la demi-droite AB.
Définition:
Une demi-droite est un ensemble infini de point ayant un extrémité ou une origine. Ce segment a pour extrémité les points A et B, il se note [AB] ou [AB].
Demi-droite d'origine A passant par le point B. (AB) c'est un segment d'extrémité A et B.