Mouvement de translation rectiligne
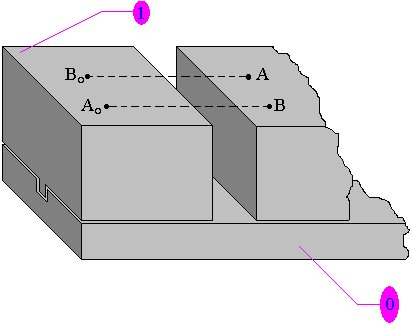
Le mouvement de 1/0 est un mouvement de translation rectiligne si à chaque instant A0B0=AB=cste et que (A0A) droite rectiligne.
Nature des trajectoires
Tous les points de 1 décrivent des trajectoires rectilignes.
Equation horaire du mouvement
A0A0=B0B=5 abscisse curviligne
Tous les points de 1 ont une équation horaire du mouvement S=f(t)
Vecteur vitesse linéaire
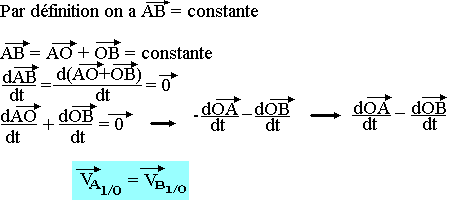
Tous les points d'un solide en translation rectiligne ont même vitesse linéaire.
Lors du mouvement de translation rectiligne d'un solide, tous les points de celui-ci ont même vitesse linéaire.
Vecteur accélération linéaire
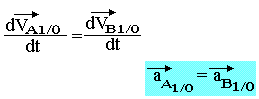
Tous les points d'un solide en translation rectiligne ont même accélération.
Mouvement de rotation au tour d'un axe fixe
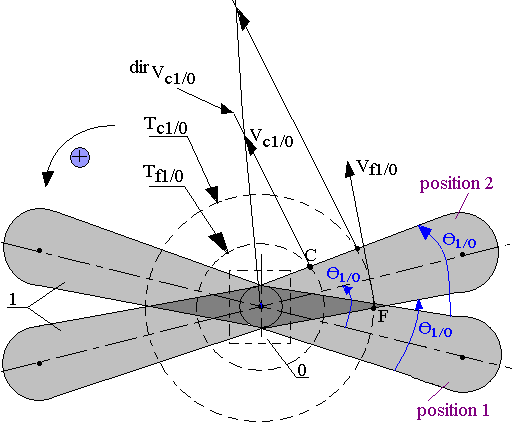
Le solide 1 est animé d'un mouvement de rotation au tour d'un axe fixe passant par I si deux points A et B de 1 restent fixes pendant le mouvement. (AB) est confondu avec l'axe du mouvement.
Nature des trajectoires
Pendant le mouvement de 1/0 tous les points décrivent des trajectoires circulaires centrées sur l'axe de rotation.
La vitesse de rotation
O1/0 angle du mouvement 1/0 est l'angle géométrique mesuré en radian.
La vitesse de rotation est la dérivée par rapport au temps de O1/0
![]()
La vitesse linéaire
Caractéristiques de VF1/0
- Point d'application: le point F
- Direction: perpendiculaire en F à (IF)
- Sens: celui du mouvement.
- La norme VF1/0=IF.W1/0
Propriétés:
- Si on a ABC des points de 1 non situés sur l'axe de rotation. On a la rotation
![]()
- Tous les points situés sur une même circonférence ont même vitesse.
Les accélérations
Accélération angulaire
![]()
Vecteur accélération linéaire
Caractéristiques de l'accélération normale
- Point d'application F
- Direction (IF)
- Norme:
![]()
Caractéristiques de l'accélération tangentielle
- Point d'application: F
- Direction: Perpendiculaire à (IF) en F
- Sens:
- Celui du mouvement si celui-ci est accéléré
- Opposé à celui du mouvement si celui-ci est décéléré
- Norme:
![]()
Mouvement plan sur plan
Le mouvement 1/0 est un mouvement plan sur plan lorsqu'il est considéré comme combinaison d'un mouvement de rotation et d'un mouvement de translation rectiligne. Un point de ce solide décrira une circonférence et l'autre point décrira une trajectoire rectiligne.
La propriété d'équiprojection
Enoncé
Soit A et B deux points d'un solide 1 en mouvement plan par rapport à un solide 0. VA1/0 et VB1/0 leur vitesse respective. La projection orthogonale VA1/0 sur AB est égale à la projection orthogonale de VB1/0 sur AB.
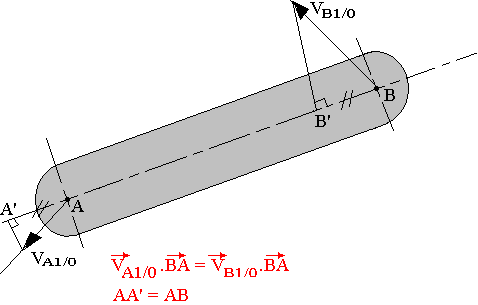
Remarques:
- Les points A' et B' sont situés du même côté par rapport au point d'application des vecteurs sur la droite (AB)
- Lorsqu'un solide est en mouvement plan, la propriété d'équilibre permet de déterminer graphiquement la vitesse d'un point (direction connue) à partir du vecteur vitesse d'un autre point entièrement connu.
Exercice d'application:
Le système bielle manivelle
O'A=40mm ; AB=128mm ; échelle 1Cm→1m/s
La vitesse de rotation de 1/0 est 100rad/s.
- Nature du mouvement 1/0
- Nature du mouvement 2/0
- Déterminer entièrement VA1/0
- Déterminer VB3/0
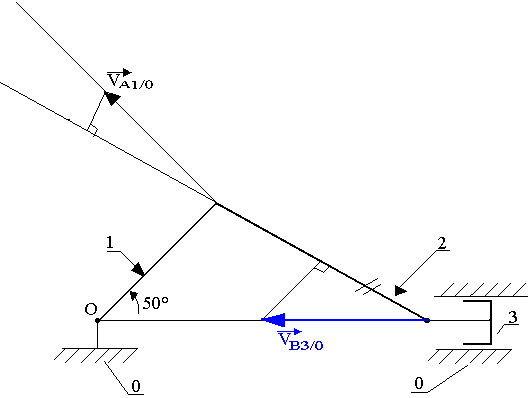
Solution:
- Le mot 1/0: mouvement de rotation de l'axe passant par 0
- Le mot 2/0 : mouvement plan sur plan
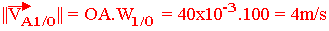
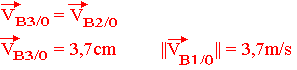
On considère le mouvement de 2 par rapport à 0.A chaque instant t il existe un point I appelé CIR tel que VI2/0=0 à l'instant t considéré.
Construction
Le CRI est situé à l'intersection des perpendiculaires aux vecteurs vitesses tracés à partir des points d'application de ces vecteurs vitesse.
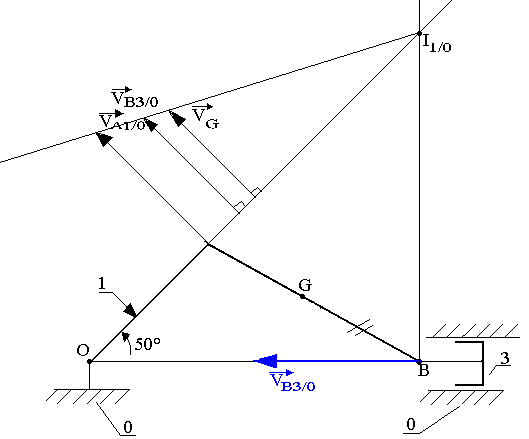
Lorsque les perpendiculaires sont parallèles le CIR se trouve à l'infini.
