Nature du courant électrique
On appelle courant électrique un mouvement d'ensemble de charge libre dans un milieu. D'après cette définition il ne peut avoir du courant électrique dans un milieu qua dans un milieu si celui-ci renferme des charges libres c'est-à-dire susceptibles de se mettre en mouvement. Lorsqu'il existe des charges libres dans un milieu, un champ électrique même de faible intensité peut les mettre en mouvement. Un tel milieu peut être soit un conducteur conventionnel (métaux et alliage), soit un semi-conducteur, soit encore un électrolyte des gaz ionisés ou même dans le voisinage de la cathode, dans le cas de l'effet thermoélectrique. Dans le cas d'un électrolyte le courant électrique est dû au double mouvement des ions positif négatifs. Les ions de plus faible masse se déplacent dans l'électrolyte plus rapide que les autres, exemple: la pile Daniel.
Production du courant électrique
Si à l'aide d'un fil conducteur, on relie deux conducteurs A et B donc les potentiels initiaux sont différents. Des charges électriques passent du conducteur du plus grand potentiel à celui de faible potentiel. Le mouvement cesse dès que l'équilibre électrostatique est atteint. Le courant électrique produit est dit transitoire c'est-à-dire de très faible durée. Pour obtenir le courant électrique qui circule le plus longtemps, les conducteurs A et B doivent être reliés à une source qui maintient leur potentiel différent (générateur électrique).
Intensité du courant électrique: densité de courant
Intensité du courant électrique
Le courant électrique étant par définition un mouvement de charge électrique. On peut caractériser le courant par la charge qui traverse une surface ds du milieu conducteur.
Soit dq la charge qui traverse une surface du milieu conducteur pendant le temps dt. On appelle intensité du courant électrique à travers la surface, le rapport di=dq/dt. L'unité est l'ampère.
Vecteur densité de courant
Cherchons la charge dq traversant un élément de surface ds dans le milieu conducteur pendant le temps dt. On remarque que ces charges animées de la vitesse V lorsqu'elles atteignent ds à l'instant t, se trouve à l'instant t+dt, à l'intérieur du cylindre de base ds et de générateur Vdt.
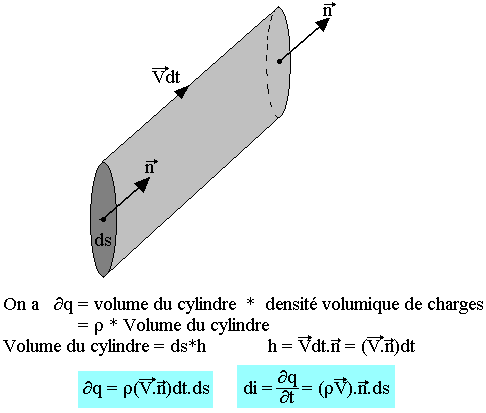
On constate que la charge qui traverse la surface ainsi que l'intensité du courant à travers cette surface s'exprime simplement à l'aide du flux du vecteur J=ÞV.
J est appelé vecteur densité du courant
![]()
On ne déduit la charge qui traverse une surface finie S dans le milieu conducteur pendant dt
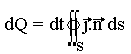
L'intensité à travers la surface S est
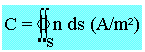
L'unité de la densité est A/m2
La densité volumique de charge Þ(M; t) des porteurs mobiles et le vecteur densité J(M,t) du courant correspondant sont liais par la loi de conservation de l'électricité. En un point M à la date t.
![]()
Dans un régime permanant (ou stationnaire), ou encore (statique), toutes les grandeurs caractéristiques du courant sont indépendant du temps, c'est-à-dire J=J(M) et Þ=Þ(M), par suite i est constant à tout instant le courant est continu, dans ces conditions divJ(M)=0.
Définitions
- Ligne de courant: C'est une ligne en tout point de laquelle le vecteur J est tangent à la ligne au courant au point M:
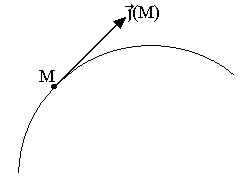
- Tube de courant: C'est un ensemble de ligne courant s'appuyant sur un même contour ferlé.
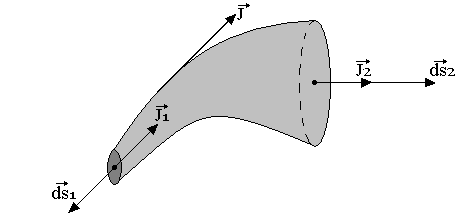
Compte tenu du théorème de GREEN HISTROVASKI, la conservation du flux de J implique l'intensité du courant est la même dans toute section droite du tube de courant.
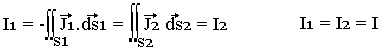
Conductivité – résistivité
Faits expérimentaux
L'expérience montre que dans un champ à température constante le vecteur densité de courant en un point est proportionnel au champ électrique en ce point.
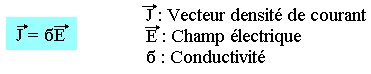
Cette relation constitue la loi d'Ohm dans sa forme locale. La constante de proportionnalité est б. La loi d'ohm est valable pour un grand nombre de conducteur usuel.
Interprétation
On sait qu'un conducteur renferme les charges libres sous l'action d'un champ électrique. Ces charges vont se mettre en mouvement, ce mouvement est toutefois gêné par la présence d'autres charges présentes dans le milieu conducteur. Ainsi dans le cas d'un métal les charges libres sont les électrons libres et le mouvement des électrons libres est généré par les ions.
Supposons qu'on puisse décrire cette force de résistance par une force de frottement de type visqueux f=bV. V étant la vitesse de la charge considérée et b une constante positive caractéristique de la substance considérée. Le mouvement d'une charge q de masse m obéit à la relation fondamentale de la dynamique.
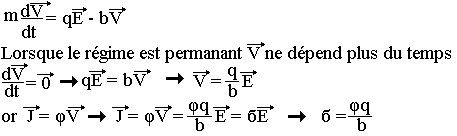
Remarque 1:
L'hypothèse de frottement visqueux conduit à la loi d'ohm certes mais ne rend pas compte de ce qui se passe effectivement pour une charge microscopique. En effet un électron libre dans un conducteur accéléré par un champ électrique subit des chocs électriques contre les ions et leurs cortèges électriques. Ces chocs modifient leur vitesse, ainsi entre deux chocs consécutifs la vitesse u d'un électron libre est telle que:
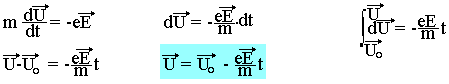
U0 représente la vitesse de l'électron immédiatement après le choc. La vitesse d'ensemble des électrons libres doit être égale à la vitesse moyenne des vitesses moyennes immédiates individuelles des électrons libres.
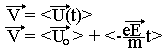
<U0>=0 car le mouvement initial des électrons est parfaitement désordonnée. La valeur moyenne d'une fonction f(t) à un intervalle de temps T est par définition
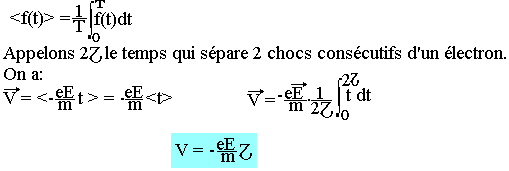
Appelons n le nombre d'électron libre du métal par unité de volume, la charge délimitée de volume est Þ=-ne par conséquent
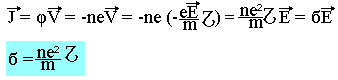
Remarque 2:
La loi d'ohm implique que l'on ait aussi V proportionnel à E. On convient de définir la constante de proportionnalité de telle sorte que V=-µE pour une charge négative.
µ est la mobilité du porteur de charge avec
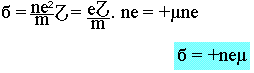
Dans le cas d'un milieu comportant deux types de porteur de charge nous aurons
![]()
Résistance d'un conducteur
Considérons un conducteur l d'extrémité A et B parcouru par un courant d'intensité I.

Si on multiplie par un scalaire k quelconque VA-VB est inchangée.
Définition:
On appelle résistance d'un conducteur ohmique la quantité R=(VA-VB)/I
On obtient ainsi l'expression générale de la loi d'ohm pour une résistance VA-VB=RI
Si on pose U=VA-VB, on obtient alors U=RI. La résistance quant à elle peut s'écrire

Remarques:
- On définit aussi la conductance d'un conducteur traditionnellement notée
- Cas d'un conducteur filiforme: Un conducteur est dit filiforme lorsque ses dimensions transversales sont faibles devant sa longueur. Les lignes de champ sont alors parallèles aux génératrices du fil.
Soit l sa longueur et soit S sa section droite on a donc:
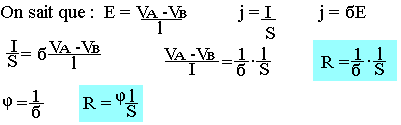
Association des conductances
On peut associer les résistances soit en série, soit en parallèle.
Association en série
Considérons trois résistances R1, R2 et R3 montées en série
![]()
Dans ces conditions les résistances sont traversées par le même courant d'intensité I, et on peut écrire la loi d'ohm aux bornes de charge résistance.
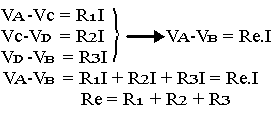
Ainsi d'une manière générale dans le cas d'un groupement en série
![]()
Association en parallèle
Considérons trois résistances R1, R2, R3 montées en parallèle.
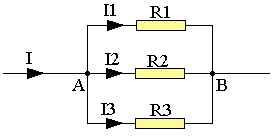
Dans ces conditions les résistances sont soumises à la même différence de potentiel mais sont traversées par les courants d'intensité différente:
VA-VB = R1I1 = R2I2 = R3I3
VA-VB = ReI
I1=(VA-VBB)/R1 ; I2=(VAVB)/R2 ; I3=(VA-VB)/R3 ; I=I1+I2+I3
1/Re=1/R1+1/R2+1/R3
On généralise aisément dans le cas d'un groupement en parallèle.
![]()
Conséquence
Diviseur de tension
Soit deux résistances R1 et R2 montées en série et parcourues par le même courant d'intensité I. Soit U la différence de potentiel aux bornes de l'ensemble et soit U' la ddp aux bornes de R2
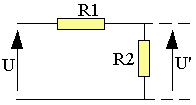
U=(R1+R2)I ; U'=R2I
U=(R1+R2)U'/R2 ; U'=R2.U/(R2+R1)
Diviseur de courant
Soient deux résistances R1 et R2 montées en parallèles
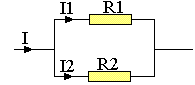
Elles sont soumises à la même ddp, U. Soient I1 et I2 les intensités traversant ces résistances.
I=I1+I2 ; U=R1I1=R2I2
I1=R2I/(R1+R2)
