Nous nous proposons d'étudier dans ce cours la réponse d'un circuit simple à excitation sinusoïdale permanente, autrement dit d'étudier plus en détail le régime forcé de certains circuits.
Cela nous donnera l'occasion d'introduire la notion de quadripôle ainsi que sa fonction de transfert qui sera très utilisé en électronique.
Généralité sur les quadripôles
Présentation du problème
Expérimentalement, le problème se pose de la manière suivante. Le circuit étudié est relié à une source de tension alternative sinusoïdale connue et on mesure la réponse aux bornes de tous ses éléments. Cette réponse est une tension mesurée par un oscilloscope cathodique où on a un voltmètre de très grande impédance d'entrée.
Le circuit étudié apparaît ainsi comme un quadripôle de présentant deux bornes d'entrée (du côté de la source de tension) et deux bornes de sortie (du côté de l'appareil de mesure)

Considérons un quadripôle soumis à une tension d'entrée Ve et parcouru par un courant d'intensité ie.
Soient VS et iS les tensions et courant de sortie:

Un quadripôle est passif lorsqu'il ne comporte aucune source de tension sinon il est actif. Nous envisagerons ici uniquement les quadripôles passifs.
Un quadripôle est très souvent caractérisé par son gain que l'on peut définir de différente manière:
- Gain en puissance: Si Pe est la puissance fournie à l'entrée et PS la puissance récupérée à la sortie du quadripôle, ce gain est P/Pe. Pour un quadripôle passif ce gain est évidemment inférieur à 1.
- Gain en tension: C'est le rapport VS/Ve
- Gain en intensité: C'est le rapport iE/ie
Fonction de transfert d'un quadripôle
D'une manière générale, le quadripôle introduit un déphasage entre les tension Ve et VS. Aussi est-il adapté d'utiliser, et non les valeurs instantanées des tensions mais les valeurs complexes associées VS et Ve.
On appelle alors fonction de transfert du quadripôle la fonction de ω que nos noterons H(jω) définie par H(jω)=VS/Ve.
Soit VS et Ve les valeurs efficaces des tensions.
Soit þ le déphasage de vs sur ve, la fonction de transfert s'écrit H(jω)=VSejþ/Ve.
A priori le rapport VS/Ve et þ dépendent de ω. Nous poserons ainsi :
H(jω) = G(ω)ejP
G(ω) = VS/Ve
G(ω) représente le gain en tension du quadripôle et nous voyons que G(ω) est simple, le module de la fonctions de transfert.
Etude de quelques exemples
Etude du quadripôle RC
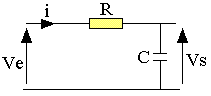
Alimentons le circuit RC ci-dessus au moyen d'une tension alternative de la forme ve=Ve√2Cos(ωt) et étudions la réponse sous la forme tension de sortie vS.
Nous supposons que l'appareil de mesure permettant de déterminer vS a une impédance infinie (de manière à négliger tout débit dans cet appareil). En notation complexe on peut alors écrire:
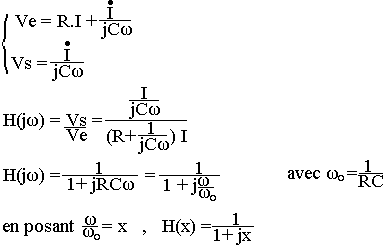
En posant ω/ω0=x ; H(x)=1/(1+jx)
Etude du gain
G(x)=1/(1+x2)½
Cette expression de G(x) montre que:
- Pour le quadripôle étudié G(x) < 1.
- G(x) aura même forme pour les quadripôle de type RC, quelque soit R et C à condition d'utiliser la variable réduite x. Une étude sommaire de la fonction G montre que la courbe représentative a la forme suivante:
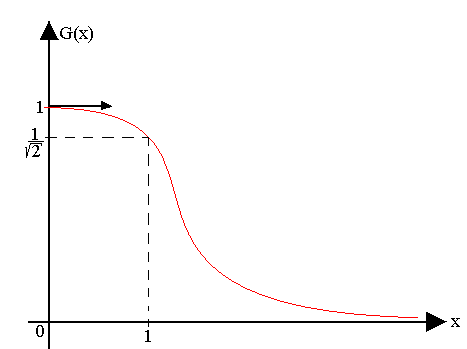
Détermination pratique : le décibel
Soit VR une tension de référence quelconque (en valeur efficace). AU moyen du voltmètre on mesure la tension à l'entrée d'un quadripôle et comme g(x)=20LogG(x) ; Ve(dB)=20Log(Ve/VR) ; VS(dB)=20Log(VS/VR)
On en déduit VS(dB)-Ve(dB)=20LogG
Ainsi le gain en décibel s'obtient par la simple soustraction des tensions et d'entrée en décibel.
Pour x=1 ; G=1/2½ g=-3dB
On a un affaiblissement à -3dB où un affaiblissement de 3dB. La valeur ω, ωC=ω0 pour laquelle x=1 est appelée pulsation de coupure.
Le quadripôle considéré constitue un filtre passe bas laissant avec une atténuation inférieure à 3dB. Les pulsations inférieurs à ω0=1/RC et atténuant d'une manière importante les pulsations supérieurs à ω0.
