Conversion d'une base à une autre
Passage d'une base "b" différente de 10 à la base 10
Il s'agit simplement d'écrire le nombre à convertir sous la forme polynomiale dans sa base "b" puis d'effectuer les calculs pour obtenir la valeur en base 10.
Conversion binaire - décimale
Exemple 1:
Convertir le nombre X1=(1101)2
Résolution:
X1 = (1101)2 = 1x23 + 1x22 + 0x21 + 1x20 = 8 + 4 + 0 + 1
X1 = (1101)2 = (13)10
Exemple 2:
Convertir le nombre X2=(1001,101)2
Résolution:
X2 = (1001,101)2 = 1x23 + 0x22 + 0x20 + 1x2-1 + 0x2-2 + 1x2-3 = 9 + 0,5 + 0,125
X2 = (1001,101)2 = (9,625)10
Conversion octale - décimale
Exemple 1:
Convertir X1 = (342)3
Résolution:
X1 = 3x82 + 4x81 + 2x80 = 192 + 32 + 2 = 226
X1 = (342)8 = (226)10
Exemple 2:
Convertir X2 = (745,05)8
Résolution:
X2 = 7x82 + 4x81 + 2x80 + 0x8-1 = 448 + 32 + 2 + 0 + 0,078125
X2 = (742,05)8 = (482,078125)10
Conversion hexadécimale - décimale
Exemple 1:
X1 = (1F2) ? ( )10
Exemple 2:
X2 = (1AOB,CD)16 ? ( )10
Passage du décimal à la base "b"
Le principe ici consiste à effectuer des divisions successives du nombre décimal à convertir par la base "b"
Exemple 1:
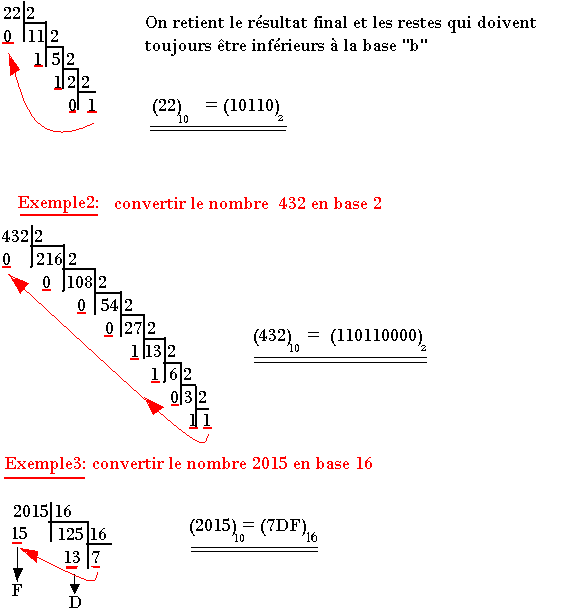
Convertir le nombre (22)10 = ( )2
Résolution:
On retient le résultat final et les restes qui doivent toujours être inférieurs à la base "b"
Conversion d'une base a une autre différente de la base 10
Première méthode
Elle consiste à faire un passage par la base 10 en suite quitter de la base 10 à la base recherchée.
Exemple: Convertir (1101)2 = (?)8
- Première opération:
(1101)2 = (13)10 - Deuxième opération:
(13)10 = (15)8
(1101)2 = (15)8
Deuxième méthode:
Elle consiste à regrouper les bits par bloc de 4 à partir de la droite en suite convertir la valeur de chaque bloc en hexadécimal (cas de la conversion binaire hexadécimal).
Le regroupement se fera par bloc de 3 bits lorsqu'il s'agira de la conversion octale.
Concours d'entrée aux grandes écoles