Tableaux des équivalences:
|
Décimal |
Binaire |
Hexadécimal |
|
0 |
0000 |
0 |
|
1 |
0001 |
1 |
|
2 |
0010 |
2 |
|
3 |
0011 |
3 |
|
4 |
0100 |
4 |
|
5 |
0101 |
5 |
|
6 |
0110 |
6 |
|
7 |
0111 |
7 |
|
8 |
1000 |
8 |
|
9 |
1001 |
9 |
|
10 |
1010 |
A |
|
11 |
1011 |
B |
|
12 |
1100 |
C |
|
13 |
1101 |
D |
|
14 |
1110 |
E |
|
15 |
1111 |
F |
|
Décimal |
Binaire |
Octal |
|
0 |
000 |
0 |
|
1 |
001 |
1 |
|
2 |
010 |
2 |
|
3 |
011 |
3 |
|
4 |
100 |
4 |
|
5 |
101 |
5 |
|
6 |
110 |
6 |
|
7 |
111 |
7 |
Exercice 1:
Convertir en hexadécimal les nombres binaires suivants
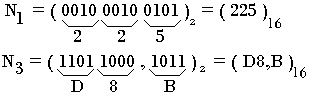
Exercice 2:
Convertir en octal les nombres binaires suivants:
Conversion d'un nombre décimal ayant une partie décimale en binaire
Le principe de conversion de la partie entière ne change pas. La partie décimale se convertit par multiplication successive de cette dernière par la base "2". On conservera à chaque fois la parie entière du résultat obtenu qui doit toujours être inférieure à la base "2".
Exemples:
Convertir (13,25)10 = (?)2
(13)10 = (1101)2
0,25 x 2 = 0,5
0,5 x = 1 1
(0,25)10 = (0,01)2
(13,25)10 = (1101,01)2
Convertir (27,625)10 = (?)2
(27)10 = 11011
0,625 x 2 = 1,25
0,25 x 2 = 0,5
0,5 x 2 = 1
(0,625)10 = (101)2
(27,625)10 = (11011,101)2
Convertir (15,3)10 = (?)2
(15)10 = 1111
0,3 x 2 = 0,6
0,6 x 2 = 1,2
0,2 x 2 = 0,4
0,4 x 2 = 0,8
0,8 x 2 = 1,6
(15,3)10 = 1111,01001
En binaire on peut compter de 0 → 2N-1
Concours d'entrée aux grandes écoles