Les vecteurs

Notion de direction et sens

Direction

Une droite représente une direction.
Étant donné une droite (AB), toute droite parallèle à (AB) détermine la même direction que (AB)

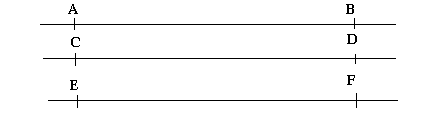
(CN) et (EF) détermine la même direction que (AB).

Sens

Soit (AB) une droite

Le sens de parcours de A vers B est le sens du couple (A,B)
Le sens de parcours de B vers A est le sens du couple (B,A)

Notion de vecteur

Soit A et B deux points du plan

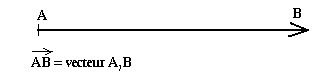
Le segment [AB] fléché en B est le vecteur AB.

Les caractéristiques d'un vecteur

Un vecteur est caractérisé par:

• Une origine
• Une direction
• Un sens
• La longueur

Exemple:

Considérons le vecteur AB:

• A est l'origine
• Sa direction est celle de (AB)
• Sens de A vers B, c'est-à-dire le sens du couple (A,B)
• Sa longueur est la longueur du segment [AB]

Egalité de deux vecteurs

On dit que 2 vecteurs sont caractéristiques c'est-à-dire même direction, même sens, même longueur.

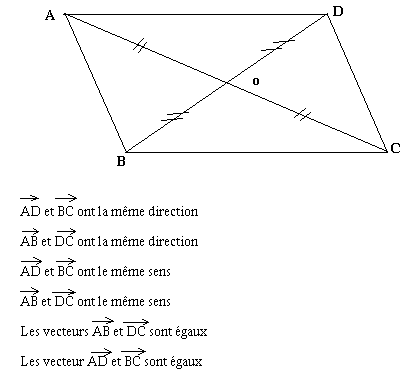
Translation et vecteurs

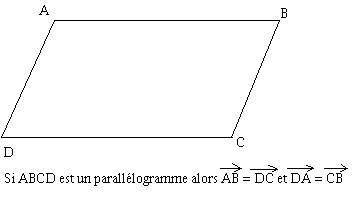
Considérons la translation qui applique A sur D et B sur C. On dira que le vecteur AD=BC est le vecteur de cette translation.
L'image de B par cette translation est C.
L'image de A par cette translation est D
Dans le cas général si M' est l'image par la translation du vecteur AB.

Vecteur et milieu d'un segment

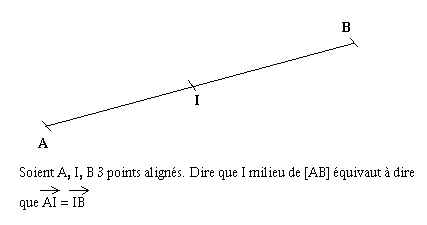
Remarque

Somme des vecteurs

A, B, C étant 3 points quelconque du plan, on pose AB+BC=AC. On dit que AC est le la somme des vecteurs AB et BC. L'égalité AB+BC=AC est appelée propriété de Chasles.
Des règles de construction de 2 vecteurs.

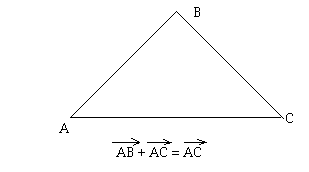
On applique la propriété de Chasles pour calculer la somme des vecteurs.

Exercice d'application

Reproduisez la figure ci-dessous et trouvez la somme des vecteurs AB et AD.

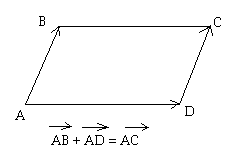
Somme de plusieurs vecteurs

Pour calculer la somme de plusieurs vecteurs:

• On peut déplacer et regrouper certains vecteurs
• On peut modifier l'ordre dans lequel on additionne les vecteurs
• On peut aussi remplacer quelques-uns des vecteurs à additionner par leur somme.