Droite et plan de l'espace

Détermination d'une droite

Détermination d'une droite

Dans l'espace 2 points déterminent une droite.
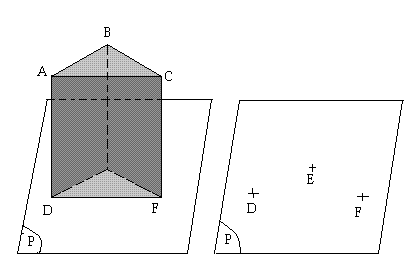
Exemple: Les 2 points A et B de la figure ci-dessus déterminent la droite (AB)

Détermination d'un plan

La base sur laquelle se dépose le prisme ci-dessus matérialise un plan.
On admet que les 3 points non alignés D, E, F déterminent le plan de la base DEF.
On note ce plan (DEF) ou (P).
Par convention on représente un plan par un parallélogramme.
Exemple: Voir le plan (DEF) représenté par la figure ci-dessus

Les droites contenues dans un plan

la figure précédente, les points C et D sont 2 points du plan ADF.
On dit que la droite (DC) est contenue dans le plan (ADF) et on note (CD)C(ADF)

Droites parallèles

Deux droites parallèles déterminent un plan.
Exemple: (AD) et (CF) sont parallèles et déterminent le plan (ADF)
Deux droites sont parallèles si elles appartiennent à un même plan et non des points communs.

Droites sécantes

Sur le prisme ABCDEF, (AB) et (AC) sont sécantes. Deux droites sécantes déterminent un plan et un seul.
Exemple: (AB) et (AC) déterminent le plan (ABC).

Plans contenant une droite

On peut trouver autant de plans que l'on veut contenant une droite donnée.
Exemple: Le bord d'une porte fixée au mur matérialise une droite (D) et à chaque position de la droite, on peut associer un plan.
On peut donc trouver plusieurs plans contenant (D)

Droites perpendiculaires

Les droites (CF) et (EF) sont deux droites perpendiculaires dans le plan (CFE).