Détermination d'une droite
Détermination d'une droite
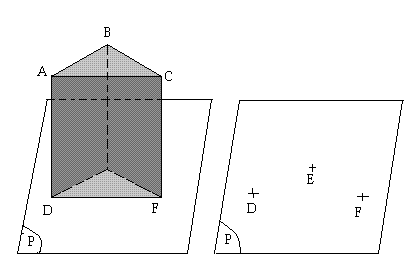
Dans l'espace 2 points déterminent une droite.
Exemple: Les 2 points A et B de la figure ci-dessus déterminent la droite (AB)
Détermination d'un plan
La base sur laquelle se dépose le prisme ci-dessus matérialise un plan.
On admet que les 3 points non alignés D, E, F déterminent le plan de la base DEF.
On note ce plan (DEF) ou (P).
Par convention on représente un plan par un parallélogramme.
Exemple: Voir le plan (DEF) représenté par la figure ci-dessus
Les droites contenues dans un plan
la figure précédente, les points C et D sont 2 points du plan ADF.
On dit que la droite (DC) est contenue dans le plan (ADF) et on note (CD)C(ADF)
Droites parallèles
Deux droites parallèles déterminent un plan.
Exemple: (AD) et (CF) sont parallèles et déterminent le plan (ADF)
Deux droites sont parallèles si elles appartiennent à un même plan et non des points communs.
Droites sécantes
Sur le prisme ABCDEF, (AB) et (AC) sont sécantes. Deux droites sécantes déterminent un plan et un seul.
Exemple: (AB) et (AC) déterminent le plan (ABC).
Plans contenant une droite
On peut trouver autant de plans que l'on veut contenant une droite donnée.
Exemple: Le bord d'une porte fixée au mur matérialise une droite (D) et à chaque position de la droite, on peut associer un plan.
On peut donc trouver plusieurs plans contenant (D)
Droites perpendiculaires
Les droites (CF) et (EF) sont deux droites perpendiculaires dans le plan (CFE).
Positions relatives d'une droite et d'un plan
Droites sécantes à un plan
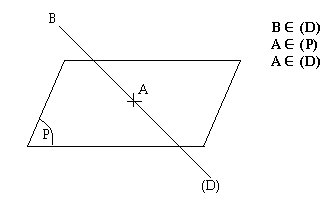
On dit qu'une droite (D) est sécante à un plan (P) lorsque (D) et (P) ont un point commun et un seul.
Droites perpendiculaires à un plan
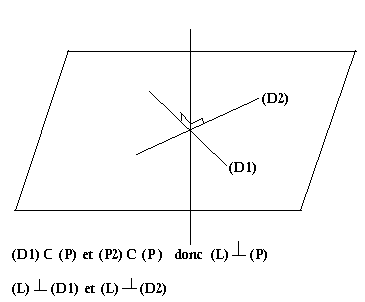
On dit qu'une droite est perpendiculaire à un plan lorsqu'elle est perpendiculaire à 2 droites sécantes de ce plan.
Propriété:
Si une droite est perpendiculaire à un plan en un point A, alors elle est perpendiculaire à toutes les droites de ce plan passant par A.
Droites parallèles à un plan
On dit qu'une droite est parallèle lorsqu'elle est parallèle à une droite du plan
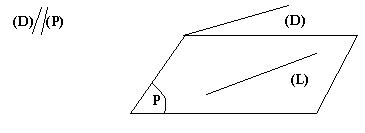
Remarque: Une droite qui n'a aucun point commun à un plan est parallèle à ce plan.
Position relative de deux plans
On dit que deux plans sont parallèles lorsqu'ils existe une droite qui est perpendiculaire à ces deux plans.
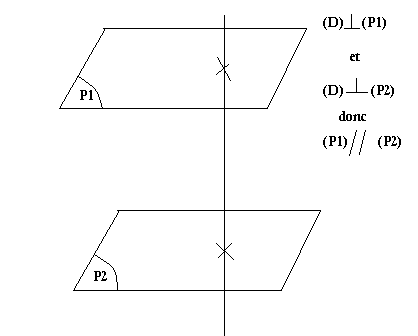
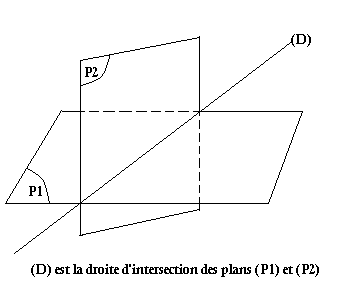
Plans sécants
On dit que 2 plans sont sécants lorsqu'ils ont une droite commune.
Plans perpendiculaires
On dit que 2 plans sont perpendiculaires lorsque l'un des plans contient une droite qui est perpendiculaire à l'autre.
Position relative de deux droites
Propriété des droites de l'espace
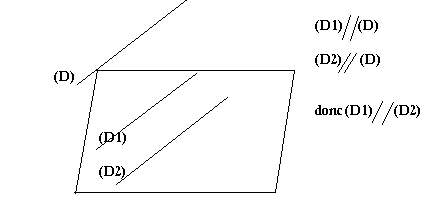
Dans l'espace, si 2 droites sont parallèles à une même troisième droite, alors elles sont parallèles entre elles.
Remarques très importantes:
Les propriétés qui s'appliquent dans chaque plan de l'espace ne sont pas toujours vérifié dans. C'est ainsi que:
- Deux droites n'ayant aucun point commun peuvent ne pas être parallèles
- Deux droites étant parallèles, on peut trouver 2 droites qui coupent l'une et ne coupent pas l'autre.
Droites coplanaires
On dit que 2 droites sont coplanaires si elles sont contenues dans un même plan.
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale