Produit scalaire
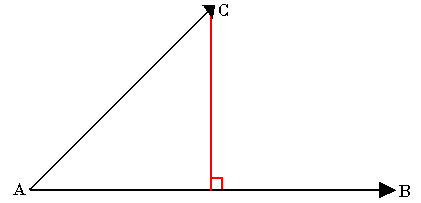
Etant donné deux vecteurs U, V et 3 points A, B, C tel que AB=U, AC=V. Le produit scalaire de U et V est le nombre réel noté U.V défini par:
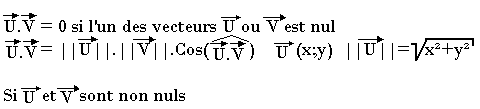
Propriétés:
Pour tout vecteur U, V, W et pour tout nombre réel K, on a:
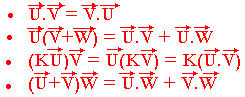
Autre expression du produit scalaire
Pour tout vecteur U et V, on a:
![]()
Expression du produit scalaire dans une base orthonormée
Soient les vecteurs u(x; y), v(x'; y')
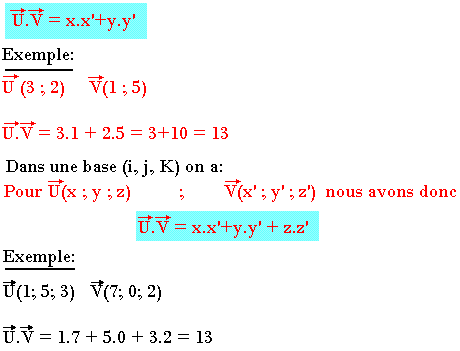
Géométrie métrique
Distance de 2 points
Soit deux points A(xA; yA; zA), B(xA; yA; zA) dans un repère orthonormé (o, i,j,k). La distance est:
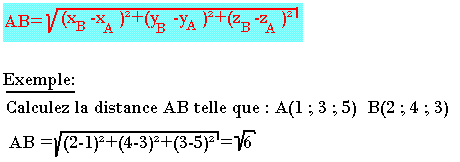
Distance d'un point à une droite
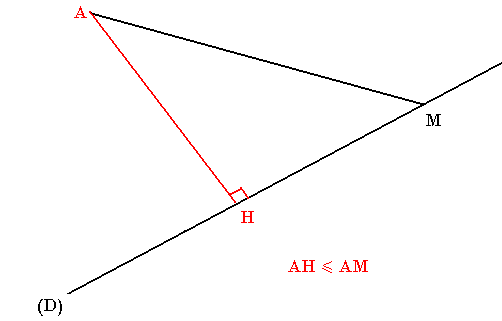
D est une droite, H le projeté orthogonal de A sur D. AH se note d(A, D), c'est cette distance que nous devons calculer.
Soit un point du plan A(xo; yo) et (D) une droite d'équation cartésienne, on a:
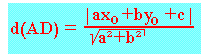
Equation du cercle
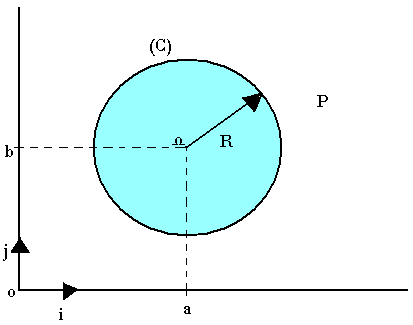
Le plan (P) étant rapporté à un repère orthonormé, une équation cartésienne du cercle de centre r de coordonnée (a; b) et de rayon R vérifié par un point M(x;y) est la relation suivante
(x-a)2+(y-b)2=R2
x2+y2-2ax-2by+c=0
Avec R2=a2+b2-c
Exemple:
Ecrire une équation du cercle de centre r(1;2) de rayon R=4
a=1 ; b=2
x2+y2-2(1)x-2(2)y+c=0 ↔ x2+y2-2x-4y+c=0
R2=a2+b2+c ↔ c=a2+b2-R2 = 1+4-16 = -11
x2+y2-2x-4y-11=0
Représentation paramétrique d'un cercle
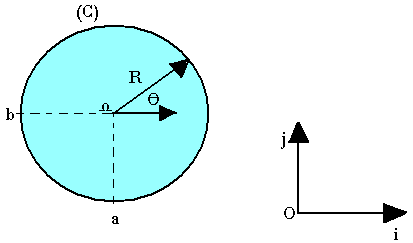
Etant donné un cercle de centre r(a; b) et de rayon R. On appelle représentation paramétrique du cercle (C) dans le repère (o, i, j), le système suivant:
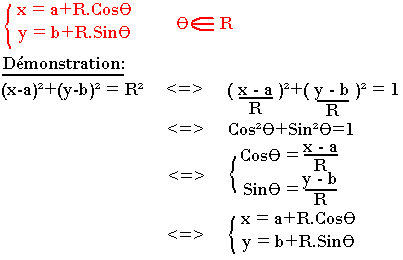
Equation cartésienne et représentation paramétrique d'un cercle
- Donnez une équation cartésienne dont la représentation paramétrique est la suivante:
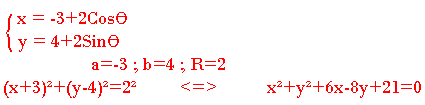
- Donnez une représentation paramétrique à partie de l'équation cartésienne suivante

Equation d'un cercle de diamètre [AB]
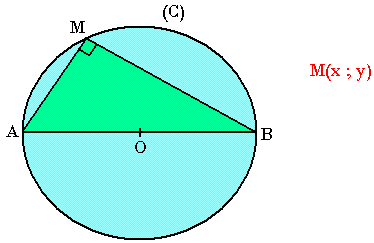
Soit deux points A(xA;yA), B(xB;yB) du plan et (C) le cercle de diamètre AB. M appartient au cercle (C)

Tangente en un point d'un cercle
Soit le cercle (C) de centre r de coordonnée (a; b), la tangente (T) à (C) au point A(x0;y0) et M(x;y) un point du plan, on a:
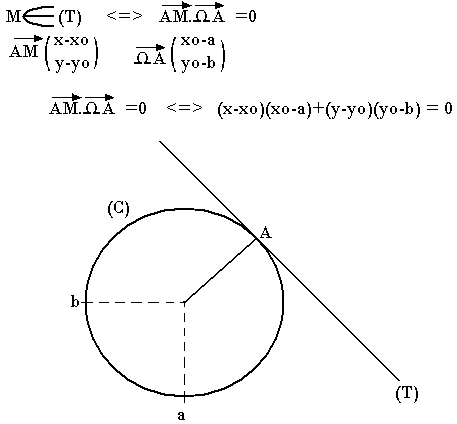
Exercice:
Soit le cercle (C') d'équation x2+y2-x+2y-3=0 et le point A(1;4).
Déterminez une équation cartésienne de la tangente à (C) au point A.
Solution:
x2+y2-4x+2y-3=0
x2+y2-2ax-2by+c=0
-2ax=-4x ↔ -2a=-4 ↔ a=2
-2by=2y ↔ -2b=2 ↔ b=-1
c=-3
(x-1)(1-2)+(y-4)(4+1)=0 ↔ -(x-1)+5(y-4)=0
-x+1+5y-20=0 ↔ -x+5y-19=0
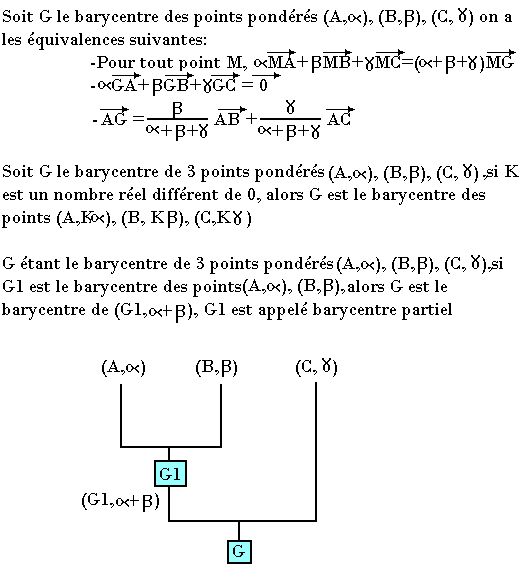
Barycentre des points pondérés
Barycentre de deux points pondérés

Exemples:
Construire le barycentre G des points pondérés (A ; 5) et (B;-8)
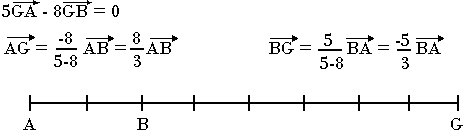
Construire le barycentre des points (A; 6) et (B; 3)
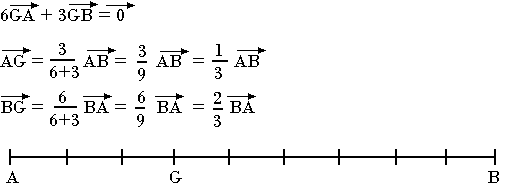
Construire le barycentre de G des points (A; 3) et B;-2)
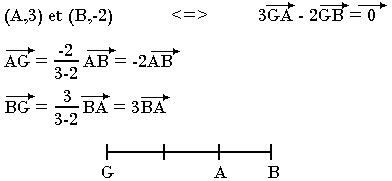
Coordonnées d u barycentre de 2 points

Barycentre de 3 points pondérés

Propriétés:
Exemple:
Soit le triangle ABC, construit le barycentre G des points pondérés (A; 2) (B; 3); (C; 6)
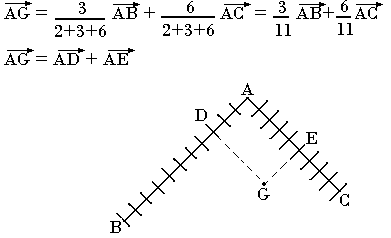
Barycentre de 4 points pondérés
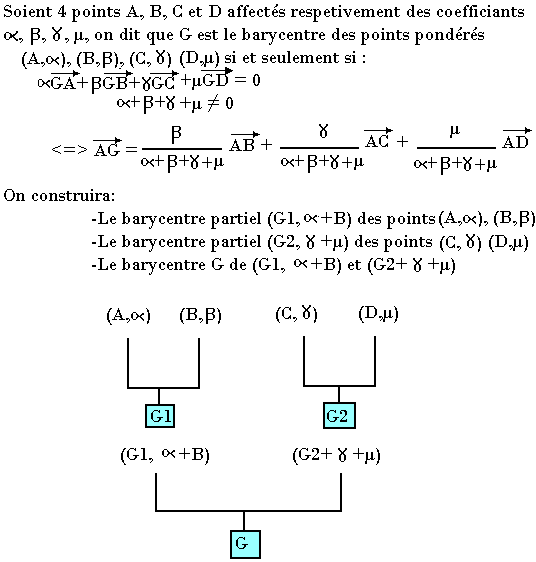
L'isobarycentre est le barycentre des points ayant le même cœfficient.
Exemple:
L'isobarycentre de 3 points pondérés (A; 1) (B; 1); (C; 1)
