Sens de variation d'une fonction
Fonction constante
Etant donné f une fonction numérique, f est dite constante sur un intervalle I si et seulement si il existe K appartenant à R tel que quelque soit x appartenant à I f(x)=K
Théorème:
f est une fonction constante si et seulement si f'(x)=0
Fonction croissante
Une fonction f est croissante sur un intervalle I si et seulement si f est dérivable c'est-à-dire quelque soit x appartenant à I f'(x) supérieure ou égale à 0
Fonction décroissante
Une fonction f est décroissante sur un intervalle I si et seulement si elle est dérivable c'est-à-dire quelque soit x appartenant à I f'(x) est inférieure ou égale à 0
Fonction monotone
Une fonction est dite monotone si et seulement si elle est soit strictement croissante soit strictement décroissante.
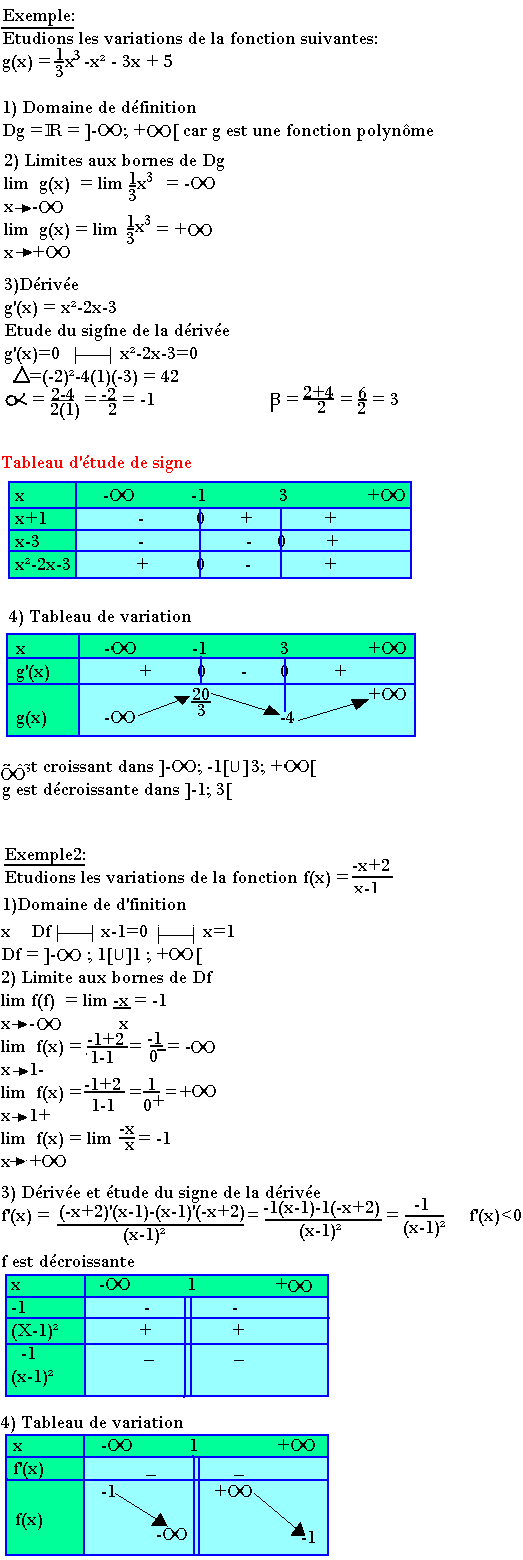
L'étude du sens de variation d'une fonction consiste à étudier sa croissance ou sa décroissante voire sa constance.
A ce titre les étapes suivantes sont très fondamentales:
- Le domaine de définition
- Les limites aux bornes du domaine de définition
- Le calcul de la fonction dérivée
- La recherche du signe de la dérivée
- Le récapitulatif dans un tableau de variation