Position de la courbe par rapport à l'asymptote

Pour déterminer la position de la courbe par rapport à l'Asymptote oblique, on étudie le signe de f(x)-y.
Si dans un intervalle donné f(x)-y est négatif, la courbe est au-dessous de l'asymptote.
Si dans un intervalle f(x)-y est positif, la courbe est au-dessus de l'asymptote

Représentation graphique

Elle se fait dans un repère orthonormé suivant une unité de longueur précise ou non.

---

La construction des asymptotes

On trace toutes les asymptotes que la courbe présente si possibles.

Les extremums

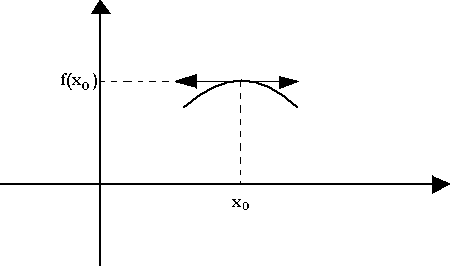
Soit f une fonction dérivable sur un intervalle I, f présente un extremum au point d'abscisse x_o appartient à I si et seulement si f'(x) s'annule en x_o et change de signe U_n extremum est un maximum ou un minimum.
La courbe de f présente un maximum en x_o si et seulement si quelque soit x appartenant à f(x) est inférieure ou égale à f(x_o)

La courbe de f admet un minimum en x_o si et seulement si f(x) est supérieure ou égale à f(x_o)

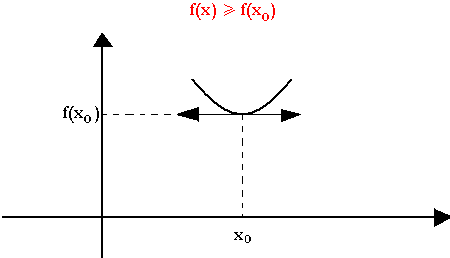
Equation de la tangente

Soit x_o l'abscisse d'un point M_o de la courbe d'une fonction. L'équation au point M₀ est y=f(x_o)+f'(x_o)(x-x_o)

Exemple:

Soit f(x) = 2x² + x -1 et x₀ = 1
Déterminez l'équation de la tangente au point x₀=1
y = f(1) + f'(1)(x-1)
f(1) = 2(1)²+ + (1) - 1 = 2 + 1 - 1 = 2
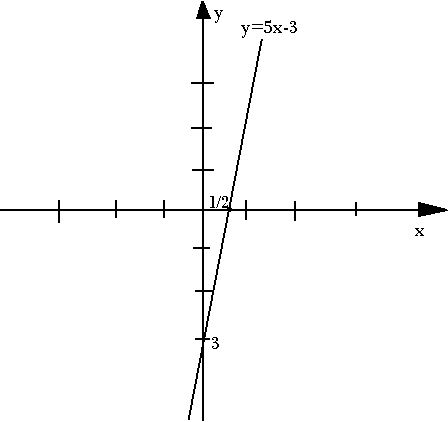
y = 2 + 5(x-1) = 2 + 5x - 5
y = 5x - 3

Plan d'étude d'une fonction

L'étude d'une fonction jusqu'à la représentation graphique se résume aux points suivants: