Fonctions associées

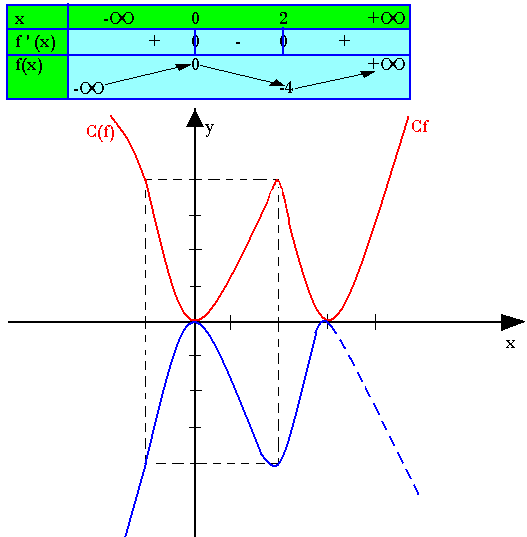
Les fonctions x → -f(x) et x → f(-x)

Ces deux fonctions étant associées à f et nous allons montrer comment leur courbe représentative se déduisent de celle de f
La courbe représentative de x →-f(x) peut se déduire de celle de f par la symétrie orthogonale d'axe (oi), car M'(x;-f(x)) est le symétrie de M(x; f(x)) par rapport à (oi).

Exemple:

f(x) = (1/4)x⁴ - x²

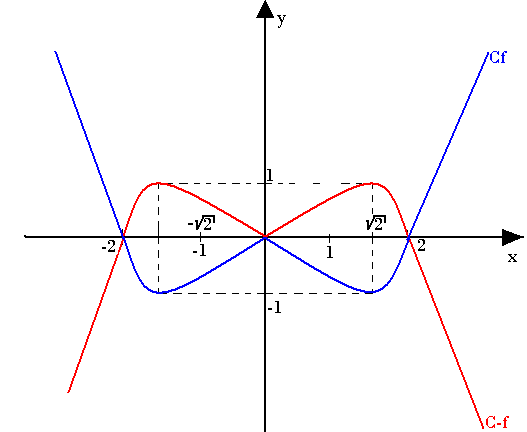
La courbe représentative de x→f(-x) se déduit de celle de f par la symétrie orthogonale d'axe (o,j) car le point M'(-x;f(x)) est le symétrie de M(x;f(x)) par rapport à (oj)

Exemple:

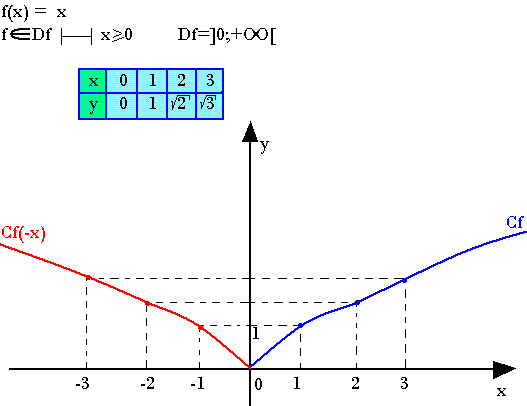
La fonction x→|f(x)|

Quelque soit x appartenant à D_f, on a:
|f(x)| = f(x) Si f(x)>0
|f(x)| = -f(x) si f(x)<0
La courbe représentative de x associée à |f(x)| est la réunion des parties des courbes d'équation respective y=f(x) et y=-f(x) situé au-dessus de (oi)

Exemple:

f(x) = x²(x-3)
x = 0
x = -2
Déduire la courbe de |f(x)| de celle de f.