Sens de variation d'une fonction

Fonction constante

Etant donné f une fonction numérique, f est dite constante sur un intervalle I si et seulement si il existe K appartenant à R tel que quelque soit x appartenant à I f(x)=K

Théorème:

f est une fonction constante si et seulement si f'(x)=0

 

---

Fonction croissante

Une fonction f est croissante sur un intervalle I si et seulement si f est dérivable c'est-à-dire quelque soit x appartenant à I f'(x) supérieure ou égale à 0

 

---

Fonction décroissante

Une fonction f est décroissante sur un intervalle I si et seulement si elle est dérivable c'est-à-dire quelque soit x appartenant à I f'(x) est inférieure ou égale à 0

 

---

Fonction monotone

Une fonction est dite monotone si et seulement si elle est soit strictement croissante soit strictement décroissante.
L'étude du sens de variation d'une fonction consiste à étudier sa croissance ou sa décroissante voire sa constance.
A ce titre les étapes suivantes sont très fondamentales:

 

---

Notion d'asymptote

Asymptote verticale

Etant donnée une fonction numérique f et D_f, sont domaine de définition soit x_o n'appartenant pas à D_f

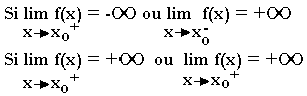
Alors la droite d'équation x_o=x est asymptote verticale à la courbe

 

---

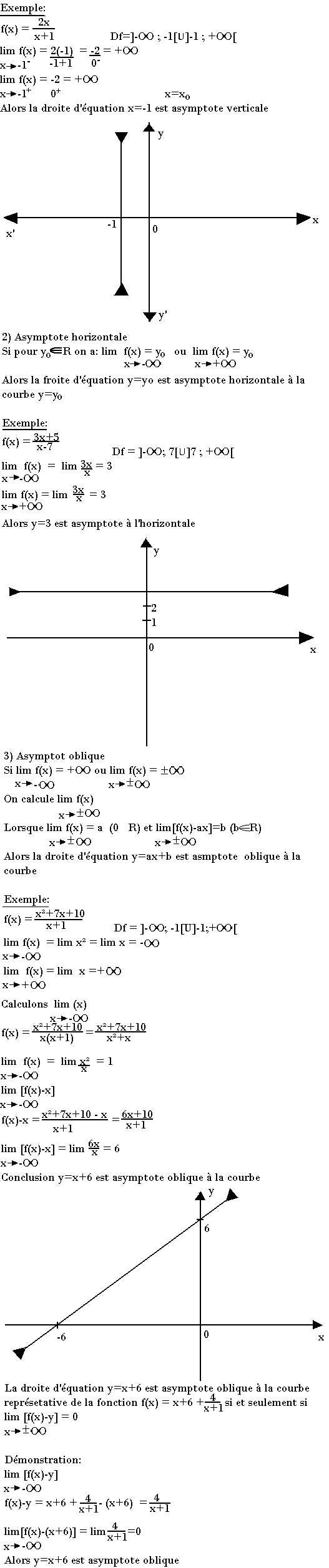
Position de la courbe par rapport à l'asymptote

Pour déterminer la position de la courbe par rapport à l'Asymptote oblique, on étudie le signe de f(x)-y.
Si dans un intervalle donné f(x)-y est négatif, la courbe est au-dessous de l'asymptote.
Si dans un intervalle f(x)-y est positif, la courbe est au-dessus de l'asymptote

 

---

Représentation graphique

Elle se fait dans un repère orthonormé suivant une unité de longueur précise ou non.

---

La construction des asymptotes

On trace toutes les asymptotes que la courbe présente si possibles.

 

---

Les extremums

Soit f une fonction dérivable sur un intervalle I, f présente un extremum au point d'abscisse x_o appartient à I si et seulement si f'(x) s'annule en x_o et change de signe U_n extremum est un maximum ou un minimum.
La courbe de f présente un maximum en x_o si et seulement si quelque soit x appartenant à f(x) est inférieure ou égale à f(x_o)

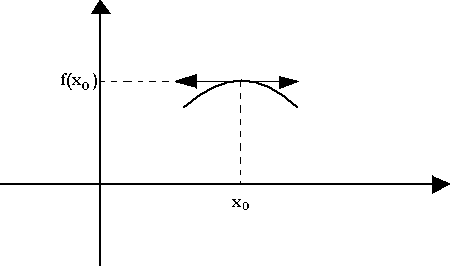
La courbe de f admet un minimum en x_o si et seulement si f(x) est supérieure ou égale à f(x_o)

 

---

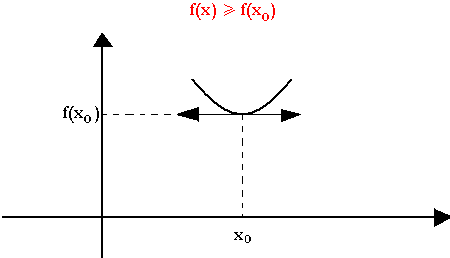
Equation de la tangente

Soit x_o l'abscisse d'un point M_o de la courbe d'une fonction. L'équation au point M₀ est y=f(x_o)+f'(x_o)(x-x_o)

Exemple:

Soit f(x) = 2x² + x -1 et x₀ = 1
Déterminez l'équation de la tangente au point x₀=1
y = f(1) + f'(1)(x-1)
f(1) = 2(1)²+ + (1) - 1 = 2 + 1 - 1 = 2
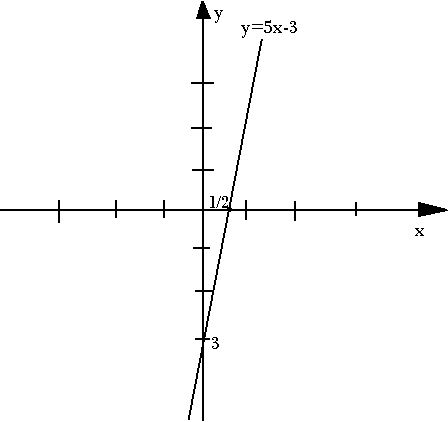
y = 2 + 5(x-1) = 2 + 5x - 5
y = 5x - 3

 

---

Plan d'étude d'une fonction

L'étude d'une fonction jusqu'à la représentation graphique se résume aux points suivants:

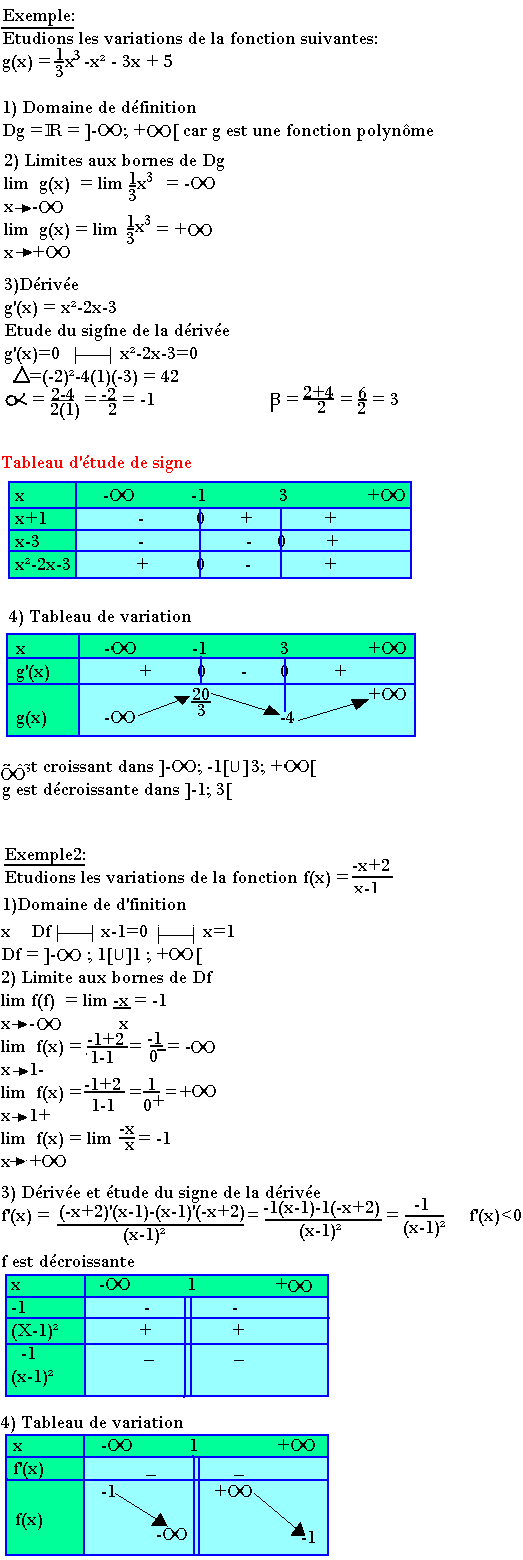
Exemple1: Cas d'une fonction polynôme

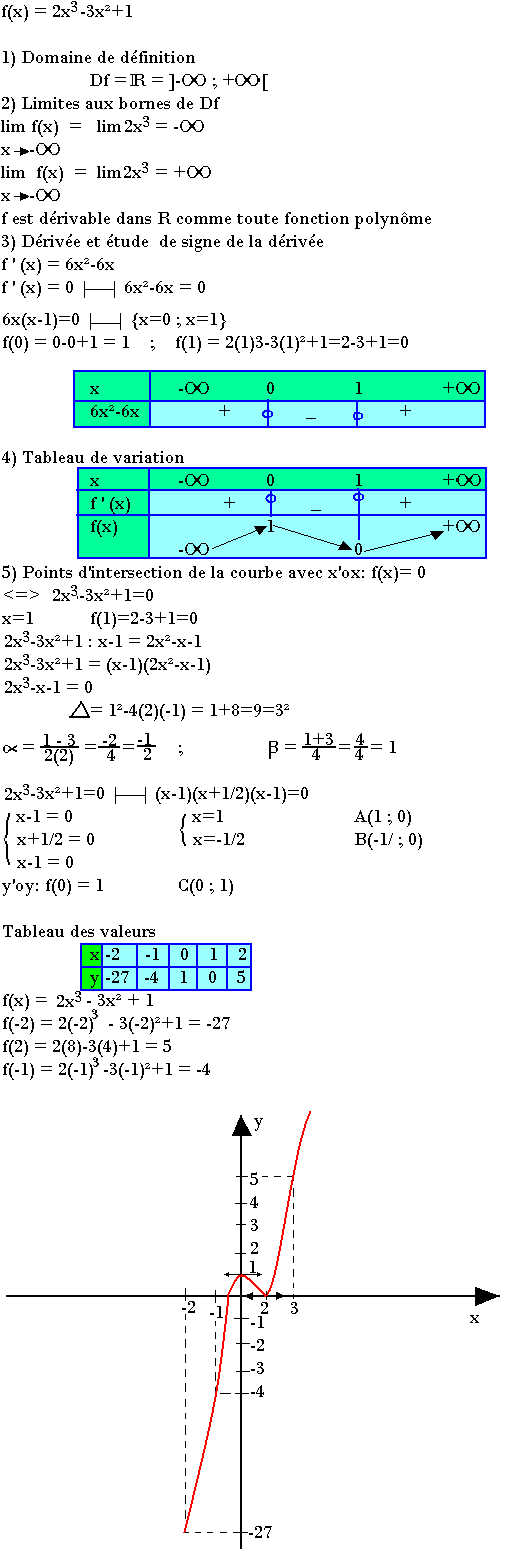
Exemple 2: Cas d'une fonction homographique

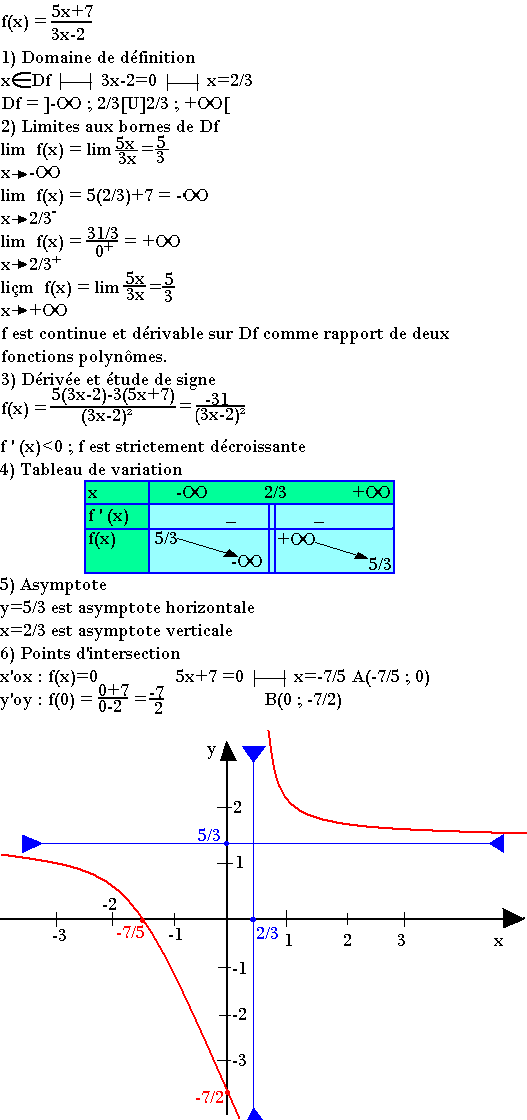
Exemple 3:

 

---

Discussion du signe et du nombre des solutions d'une équation

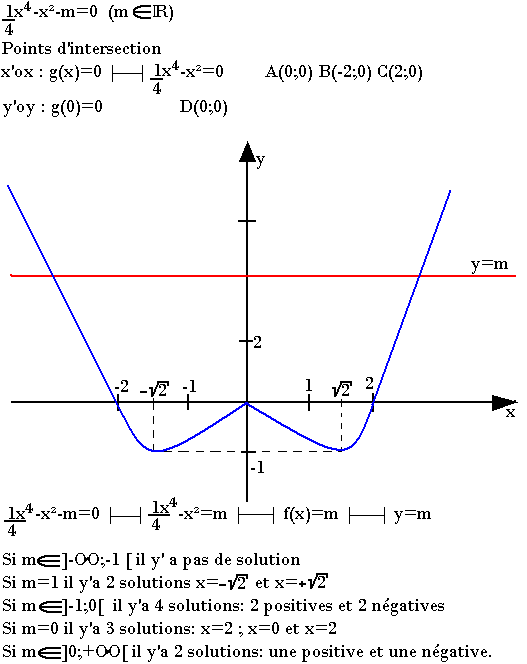
On donne une fonction g(x) = ¼x⁴ - x²
Tracez la courbe de cette fonction et discutez du signe et du nombre de solution de l'équation

 

---

Centre de symétrie et axe de symétrique d'une courbe

Généralités

Soit M(x; y) un point de la courbe C_f de la fonction f. Soit A(a; b) un point quelconque du plan rapporté à un repère orthonormé (o,i,j). Si M a pour coordonnée (X,Y) dans le nouveau repère (A,i,j), on a:
x = a + X
y = b + Y
Dans la relation y=f(x), on remplace y par b+y et x par a+X pour obtenir b+Y=f(a+X) ; Y=f(a+X)-b, cette nouvelle égalité détermine une nouvelle fonction g dans le nouveau repère (A,i,j) où Y=g(X) ; g(X)=f(a+X)-b

Théorèmes:

Si la nouvelle fonction e est impaire c'est-à-dire quelque soit x appartenant à D_g -X appartenant à D_g et g(-X)=-g(X) alors le point A(a;b) est un centre de symétrie de la courbe C_f
Si la nouvelle fonction g est paire c'est-à-dire quelque soit x appartenant à D_g -X appartient à D_g , g(-X)=g(X) alors la droite d'équation x=a est un axe de symétrie de la courbe C_f.

 

---

Exemple 1

Montrer que A(0;1) est un centre de symétrique de la courbe de la fonction f définie part f(x)=x³+1
f(x) = x³ + 1 ;  A(0;1)
x = 0 + X
y = 1 + Y
y = f(x) ↔ 1 + Y = f(X)
↔ 1 + Y = X³ + 1 ↔ Y = X³
↔ g(X) = X³
g(-X) = (-X)³ = -X³ = -g(X)
g(-X) = -g(X) alors g est impaire et A(0;1) est un centre de symétrie à la courbe.

 

---

Exemple 2

Montrez que la courbe de la fonction f(x)=x²-5x+4 admet un axe de symétrie au point A(5/2;-9/4)
f(x) = x² - 5x + 4 et A(5/2;-9/4)
x = 5/2 + X
y = -9/4 + y
y = f(x) ↔ -9/4 + Y = f(5/2+X)
↔ -9/4 + Y = (5/2+X)² - 5(5/2+X) + 4
↔ Y = X² - 25/2 + 9/4 + 25/4 + 4 ↔ Y = X²
↔ g(X) = X²
g(-X)=(-X)²=X²=g(X) ↔ g(-X)=g(X) alors g est paire et la droite x=5/2 est l'axe de symétrie pour la courbe.