Le cercle trigonométrique
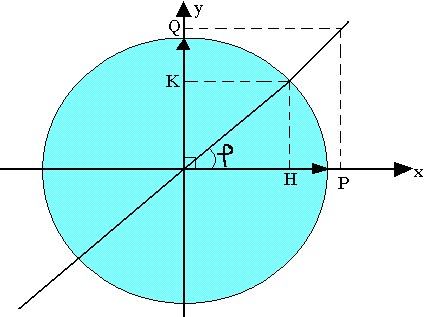
On appelle cercle trigonométrique le cercle de centre O et de rayon 1
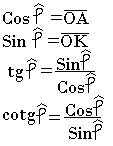
Mesure des angles
La mesure en radian d'un angle Þ est tout réel x pour lequel on a O(x)=Þ
Théorème:
Soit Þ un angle et x une mesure de Þ, un réel x' est une mesure de Þ si et seulement si il existe un entier relatif K tel que x'=x+2Kπ
Mesure principale d'un angle
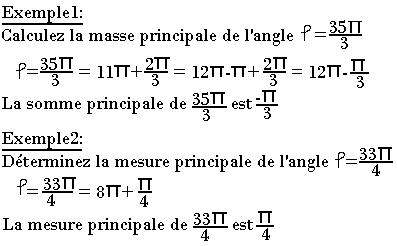
Mesure d'un angle en degré
Soit y une mesure en degré de l'angle Þ, x est une mesure en radian de l'angle Þ si et seulement si x=πy/180
Mesure d'un angle en grade
Soit y' une mesure en grade de Þ, x est une mesure en radian Þ si et seulement si x=πy'/180
Equation trigonométrique
Formule de trigonométrie
Soient les nombres réels a, b
Cos(a-b) = Cosa.Cosb + Sina.Sinb
Cos(a+b) = Cosa.Cosb - Sina.Sinb
Sin(a-b) = Sina.Cosb - Sinb.Cosa
Sin(a+b) = Sina.Cosb + Sinb.Cosa
Cos2a = Cos2a - Sin2a
Sin2a = 2Sina.Cosa
Cos2a + Sin2a = 1
Sin2a = ½(1-Cos2a)
Cos2a = ½(1-Cos2a)
Equation Cosx=a (a appartenant à l'ensemble R)
L'ensemble des valeurs de la fonction cosinus est [-1; 1]
- Si a n'appartient pas à [-1; 1], l'équation Cosx=a n'a pas de solution dans R
- Si a appartient à [-1; 1], il existe au moins un réel x0 pour lequel Cosx0=a
Théorème:
Si a appartient à [-1; 1], il existe au moins un nombre α et si a est un nombre entier relatif donné, on a:
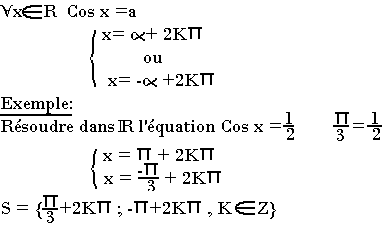
Equation Sinx=b (b appartenant à l'ensemble R)
L'ensemble des valeurs de la fonction sinus est le segment [-1; 1]
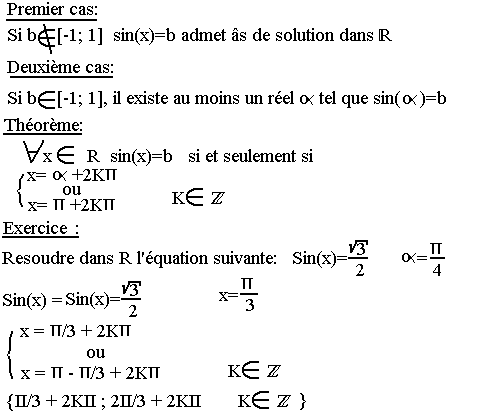
Equation tanx=c (c appartenant à l'ensemble R)
Théorème:
Quelque soit le nombre réel donné, il existe au moins un réel α tel que
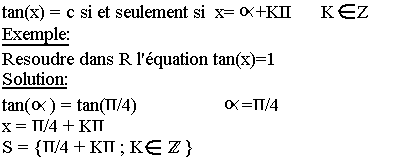
Equation aCosx+bSinx+c=0
Transformation de aCosx+bSinx
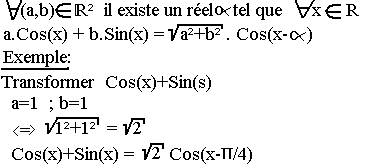
Résolution de l'équation aCosx+bSinx+c=0
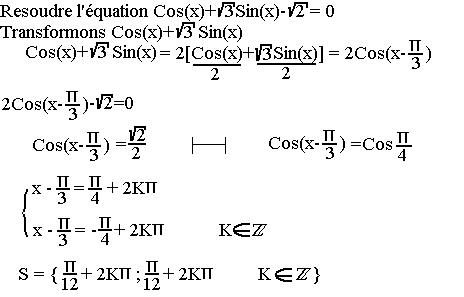
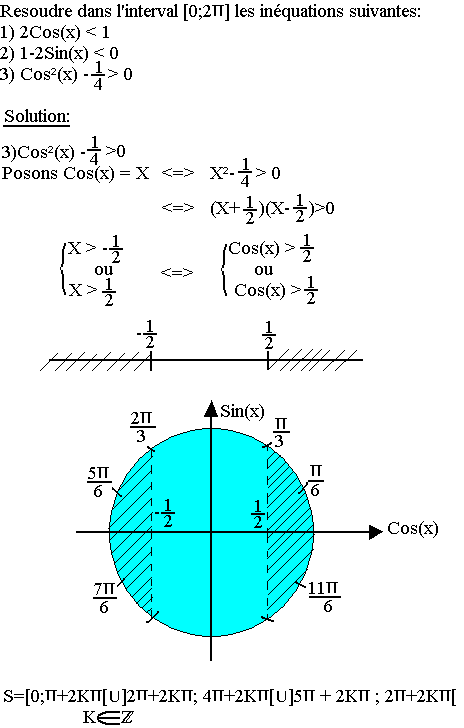
Inéquations trigonométriques
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale