Généralités
La compression est une opération qui consiste à réduire la taille occupée par les données numériques, audio ou audio-visuelles. Son principe général consiste à éliminer les informations redondantes et non significatives des données. La problématique de la compression résulte de la taille limitée de la bande passante du réseau Internet qui n'était pas conçu à la base pour recevoir un flot incessant d'image, de données audio visuels et de communications téléphoniques. Les critères d'évolution des méthodes de compression sont:
- La qualité de la reconstitution de la donnée source
- Le taux de compression.
- La rapidité du codeur/décodeur (codec).
Les problèmes liés à la compression
Le contrôle de débit
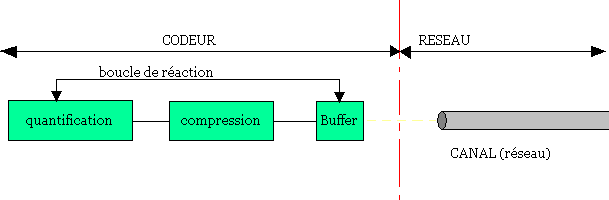
A débit constant, il peut y avoir un risque de débordement si une crise de fluidité intervient dans le réseau.
A débit variable, il peut y avoir un risque de conflit entre le codeur et le décodeur.
Les pertes dans le réseau
La perte de certaines données comme les en-têtes peuvent avoir des conséquences grammatiques sur le comportement du décodeur.
Run Lenght Encoding : RLE
C'est le plus simple des algorithmes de compression, il consiste à quantifier un seuil S0 fixé.
Exemple
Soit le texte source (P) suivant: [AAAAALBBCCCCDE] taille de (p)=14
- Fixons le seuil S0=3, on aura compress_P=[A(5)LBBC(4)DE]
taille[compress_P] = 9.
Taux de compression = [taille(P)-taille(compress_p)]/taille(P)
Taux de compression = (14-9)/14 = 35% - Fixons Seuil: S0=2
On aura compress_P = [A(5)LB(2)C(4)DE].
Taille[compress_P] = 9
Taux de compression = 35%
Exercice:
Décompressez [C(p)], Si C(P)=[00010(00101)01011(0011)10010(00100)10101(00011)11010(00100)]
Solution:
P = [B(5)K(3)R(4)U(3)Z(4)]
P = [BBBBKKKKKKKRRRUUUZZZZ]
Taux de compression = (23-10)/23 = 13/23 = 56,5%
Compression de HUFFMAN
C'est un algorithme de codage utilisé pour la compression des données (caractères, mots) son principe:
- Connaitre la taille totale du volume des données
- Affecter des codes inversement proportionnels à la fréquence des caractères contenus dans les données (haute fréquence implique codage souple)
Exemple
Texte source:
T : [aaakea befafm afakfk kfkede mdakfm]
taille(T) = 30
Fréquence:
a = 8/30 = 27%
k = 6/30 = 20%
e = 4/30 = 13%
b = 1/30 = 3,3%
f = 6/30 = 20%
m = 3/30 = 10%
d = 2/30 = 6,66%
On classe par fréquence croissante:

Compression de HUFFMAN pour les caractères
Soit le texte à compresser: T = [COMMENT_ÇA_MARCHE]
On ava supposer que les caractères de T sont données en ACII, méthode de HUFFMAN:
- On classe les caractères par fréquence décroissante
- On divise la liste ainsi obtenue en 2 sous groupes S1 et S2 dont la somme des fréquences internes respectives:
![]()
Application:
|
Caractères |
Apparitions |
Fréquences |
|
c |
2 |
11,6% |
|
O |
1 |
5,88% |
|
M |
3 |
17,64% |
|
E |
2 |
11,76% |
|
N |
1 |
5,88% |
|
T |
1 |
5,88% |
|
_ |
2 |
11,76% |
|
A |
2 |
11,75% |
|
R |
1 |
5,88% |
|
H |
1 |
5,88% |
|
Ç |
1 |
5,88% |
- Construisons une partition en 2 variables:
Le caractère à plus haute fréquence (M) n'a pas le plus petit codage, car il n'a pas été initialisé dans le sous groupe de moindre poids.
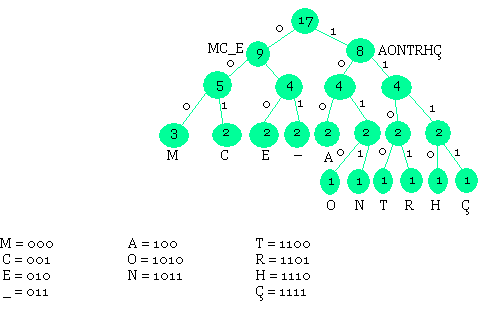
M = [COMMENT_ÇA_MARCHE]
Taux de compression de M:
Chaque caractère codé en ASCII occupe 8 bits.
![]()
Chaque caractère du texte source a la taille suivante:
|
X |
& |
Taille unitaire |
Taille totale |
|
X1 |
C |
1 |
2 |
|
X2 |
O |
4 |
4 |
|
X3 |
M |
1 |
3 |
|
X4 |
E |
2 |
4 |
|
X5 |
N |
4 |
4 |
|
X6 |
T |
4 |
4 |
|
X7 |
_ |
2 |
4 |
|
X8 |
Ç |
4 |
4 |
|
X9 |
A |
3 |
6 |
|
X10 |
R |
4 |
4 |
|
X11 |
H |
4 |
4 |
Taille (en binaire) du texte source 17x8=136bits

Théorème de l'entropie

Exemple
Soit le texte en clair "Le_codage_des_informations_utilise_du_binaire"
- Classer par ordre d'apparition chaque caractère du texte
- Déterminez l'entropie de chaque caractère.
Solution
Classons par ordre d'apparition chaque caractère du texte.
|
L |
E |
_ |
C |
O |
D |
A |
G |
S |
I |
N |
F |
R |
M |
T |
U |
B |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||||
|
1 |
1 |
1 |
||||||||||||||
|
1 |
1 |
1 |
||||||||||||||
|
1 |
1 |
Taille totale (en décimal): 45
Donnons l'entropie de chaque caractère:
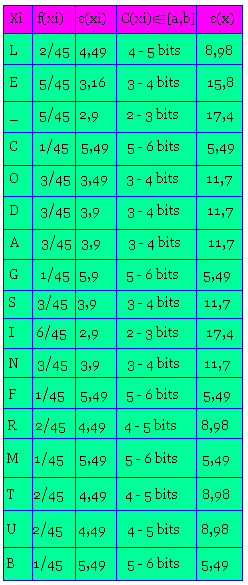
Entropie totale:
Soit (T) un texte en claire utilisant P caractères (X1, X2, X3,... XP) d'occurrence respective n1, n2, n3, ... nP alors l'entropie totale du texte (nombre total de digits qu'occupera le texte après compression).
![]()
Taux moyen de compression
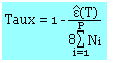
Application:
- Déterminez le taux de compression de l'exercice précédent
- Déterminez les codes de chacun des caractères (ressortir l'arbre pour sortir les codes)
Solution:
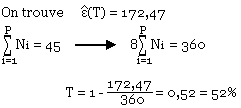
Compression et décompression d'une matrice : méthode de RLE (Run Lengle Ending)
Objectif
On souhaite décompresser une information en binaire correspondant à une matrice 16x4 (rouge, noir, gris, blanc)
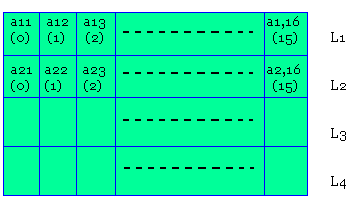
Le wagon chiffrant une case de la matrice est un double mot de 16 bits codé en binaire et divisé en 5 labels ou étiquettes.

Etiquette (A): bit (0)
Bit de fin de texte.
A=0 ; le caractère lu est dernier du texte
Etiquette (B): bit 2
Position du caractère sur la colonne de la matrice. Il faut prendre 16 valeurs de 0000 à 1111.
Etiquette (L): bits (6) et bit(7)
Indique la ligne du caractère lu, prend 4 valeurs: L1=00 (première ligne) ; L2=01 ; L4=11
Etiquette (C) : bit(8) et (9)
Indique la couleur du caractère lu, prend =4 valeurs: noir=00 ; blanc=01 ; gris=10 et rouge=11
Etiquette (R) : bits (10) à (14)
Indique le nombre de répartition du caractère lu en allant vers la droite de la ligne considérée et recommençant à gauche de la ligne suivante (LK+1).
Il peut prendre 32 valeurs de (00000) à (11111).
Etiquette (E): bits (15)
Pour les caractères d'ordre 2K-1 on a E=1. Pour les caractères d'ordre 2K on a E=0 et lorsque A=0, on a toujours E=0.
Il indique le nouveau caractère.
Exercice d'application
Soit le train d'information, comprenant un tableau en couleur (4lignes*16colonnes).
NB: On lit ce tableau de bas vers le haut.
|
26 |
0111 1111 |
0000 0010 |
||
|
24 |
1010 0011 |
1100 0110 |
1010 1011 |
0000 0111 |
|
22 |
1010 0011 |
1000 0010 |
1001 0111 |
1100 0111 |
|
20 |
1001 0011 |
1000 0010 |
1000 1011 |
1100 0101 |
|
18 |
1010 1010 |
0000 1000 |
1001 0110 |
1000 0111 |
|
16 |
1010 1010 |
0000 0110 |
1001 0110 |
1000 0011 |
|
14 |
1001 0110 |
1100 0110 |
1001 0010 |
1000 0011 |
|
12 |
1000 1010 |
1100 0100 |
1011 1001 |
0000 1001 |
|
10 |
1010 1101 |
1000 0110 |
1010 1001 |
0000 0011 |
|
8 |
1001 0101 |
1000 1010 |
1000 1001 |
1100 0101 |
|
6 |
1010 1000 |
0000 1000 |
1011 0100 |
1000 0111 |
|
4 |
1010 1000 |
0000 0110 |
1001 0100 |
1000 1011 |
|
2 |
1000 1000 |
0100 0100 |
1000 0000 |
0000 0101 |
Remplir la matrice originale (M)
|
L1 |
N |
N |
B |
B |
G |
G |
G |
G |
G |
N |
N |
N |
G |
G |
G |
|
|
L2 |
R |
R |
G |
G |
G |
G |
G |
N |
G |
G |
G |
N |
N |
|||
|
L3 |
N |
N |
R |
|||||||||||||
|
L4 |
