Page 1 sur 4
Généralités
Définitions
Vocabulaire
Une application linéaire de E vers F (E différent de F) est un homomorphisme de E vers F.
Si fEF est une bijection de E vers F on dira fEF est un Isomorphisme de E vers F.
Supposons fEF application linéaire définie dans E1 f est un endomorphisme dans E. Finalement un endomorphisme bijectif sera appelé un automorphisme.
Propriétés remarquables
Soit BE une base de E.
Si fEF est injective alors
- L'image par fEF d'un système libre de E est un système libre de F
- La matrice MEF(f) existe et est inversible
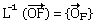
- Rang MEF(f)=dimE=N
fEF n'est pas injective alors
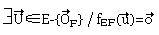
- Le déterminant de la matrice MEF(f) est nul
- Rang MEF(f)<N
Exercice d'application
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale