B^N=P^-1A^NP

Soit f une application linéaire de E vers F dont les matrices associées relativement à deux bases B et B' de E sot A_B(f) et B'_B(f) respectivement. Nous avons établi l'égalité B_B'(f)=P^-1A_B(f)P où P est la matrice de passage de base B à la base B'.
Supposons l'existence d'une application linéaire:

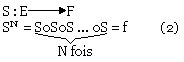
La matrice associée à S^N dans la base B étant H^N_B(S^N) , alors (1) et (2) donne B_B'(f)=P^-1H^N_B(S^N)P (3)
On peut poser W^N (S^N) la matrice de S^N dans la base B'.
L'égalité (3) devient W_B'^N=P^-1H_N^NP (2)

Exercice:

Soit E₄ un espace vectoriel de dimension 4 rapporté à sa base canonique:

Solution: