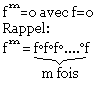---

Image et noyau d'une application linéaire

Soit f une application linéaire de E vers F, on définit les sous espaces suivants:

Images de f

Soit Im(f) le sous espace vectoriel de F définit de la façon suivante:

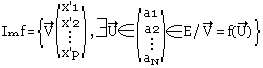
C'est l'ensemble des images obtenues par f

Caractéristiques de I_m(f)

Si f est injective, alors dim(Imf) = rangf < dimF
Si f n'est pas injective, alors dim(Imf) = rangf < dimF
Si F=E alors:

Noyau de f

Soit Ker(f) le sous espace vectoriel de E définit par:

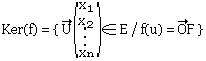
C'est le noyau de f ("Ker(f)")

Caractéristiques de Ker(f)

Si f est injective alors dim(Ker(f)) = 0 alors Ker(f)={0_E}
Si f n'est pas injective dim(Ker(f)) appartient à l'intervalle [1;N]

Exercice 1:

Soit f un endomorphisme de E₂ vérifiant:

Solution

Exercice 2

Soit E₃ un espace vectoriel de dimension 3 rapporté à sa base caractéristique:

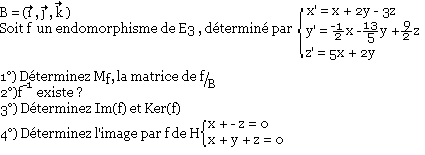
Solution

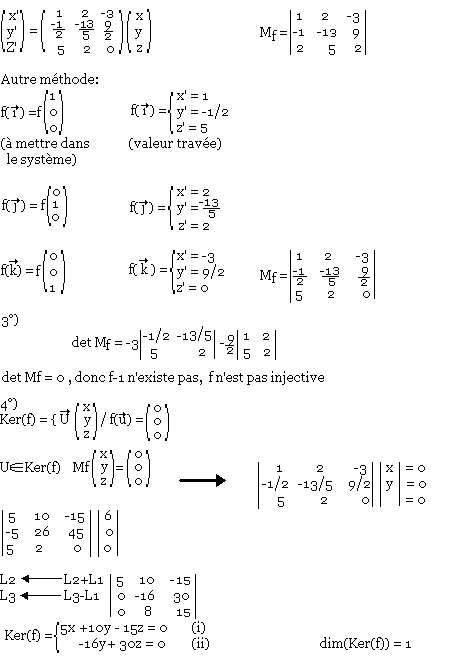
Théorème de Laplace

Soit un système d'équation à K inconnues, posons R=rang(S)
La solution de (S) comportera (N-R) paramètre à choisir, paramètre inconnus.

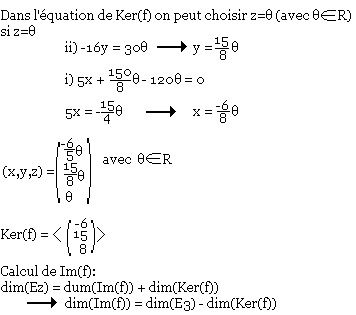
Théorème de conservation de la trace

Soit M_B la matrice d'une application linéaire, f de E_N⟶H écrit dans une base B de E_N

On appelle trace de M_B la somme des termes situés sur le diagonale de M_B notation:

Propriété

Considérons une base de E_N, B'₁, B'₂,..., B'_N, alors les différentes matrices de f relativement à B'_i tr(M'₁)=tr(M'₂)=...tr(M'_m)

Application linéaire nilpotent d'ordre n

Une application linéaire f est dite "Nilpotente" s'il existe m>0.