Compression et décompression d'une matrice : méthode de RLE (Run Lengle Ending)

Objectif

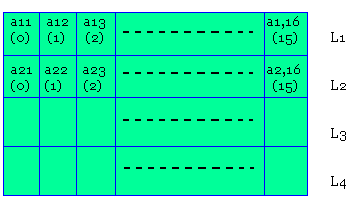
On souhaite décompresser une information en binaire correspondant à  une matrice 16x4 (rouge, noir, gris, blanc)

Le wagon chiffrant une case de la matrice est un double mot de 16 bits codé en binaire et divisé en 5 labels ou étiquettes.

Etiquette (A): bit (0)

Bit de fin de texte.
A=0 ; le caractère lu est dernier du texte

Etiquette (B): bit 2

Position du caractère sur la colonne de la matrice. Il faut prendre 16 valeurs de 0000 à  1111.

Etiquette (L): bits (6) et bit(7)

Indique la ligne du caractère lu, prend 4 valeurs: L₁=00 (première ligne) ; L₂=01 ; L₄=11

Etiquette (C) : bit(8) et (9)

Indique la couleur du caractère lu, prend =4 valeurs: noir=00 ; blanc=01 ; gris=10 et rouge=11

Etiquette (R) : bits (10) à  (14)

Indique le nombre de répartition du caractère lu en allant vers la droite de la ligne considérée et recommençant à  gauche de la ligne suivante (LK+1).
Il peut prendre 32 valeurs de (00000) à  (11111).

Etiquette (E): bits (15)

Pour les caractères d'ordre 2K-1 on a E=1. Pour les caractères d'ordre 2K on a E=0 et lorsque A=0, on a toujours E=0.
Il indique le nouveau caractère.

Exercice d'application

Soit le train d'information, comprenant un tableau en couleur (4lignes*16colonnes).
NB: On lit ce tableau de bas vers le haut.

Remplir la matrice originale (M)