Mesure d'un angle
Angles
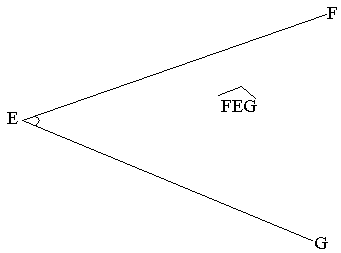
Les deux demi-droite [EG] et [EG] ayant la même origine E forment un angle que l'on note FÊG ou GÊF ou enfin Ê.
E est donc le sommet de cet angle.
Dans l'écriture de l'angle FÊG, la lettre qui désigne le sommet de l'angle se trouve entre les deux autres lettres.
Angles particulières
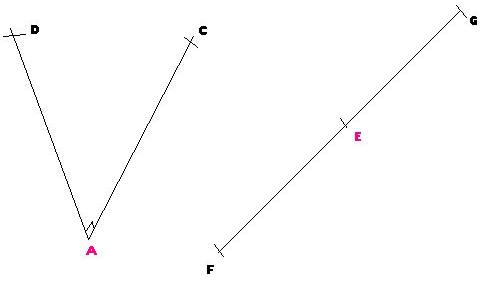
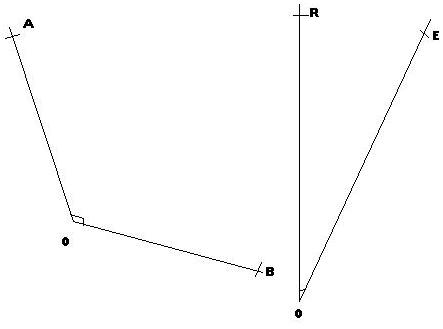
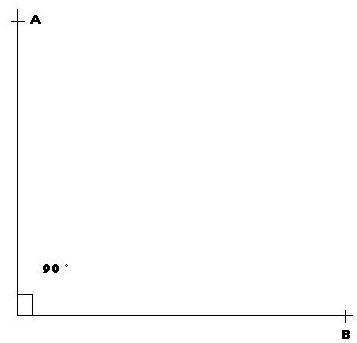
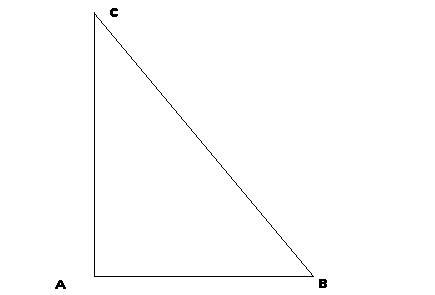
Dans la première figure les segments [AC] et [AB] sont perpendiculaires, ils froment donc un angle droit, par contre les segments [EF] et [EG] de la deuxième figure sont opposées, ils forment un angle plat.
Mesure d'un angle
Exemple:
L'unité de mesure d'un angle est le degré. L'instrument servant à mesurer un angle est le rapporteur qui est gradué en degré et s'obtient en partageant la moitié d'un cercle en 18 parties égales.
Soit la figure ci-dessous
L'angle AÎB où Î est un angle droit qui a pour mesure 90°.
Un angle est dit plat, si sa mesure est de 180°. Tout angle est dit plat, si la mesure est comprise entre 0° et 90°. Si la mesure d'un angle est comprise entre 90° et 180°, elle est appelée angle obtus
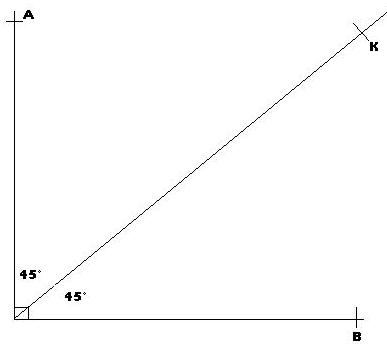
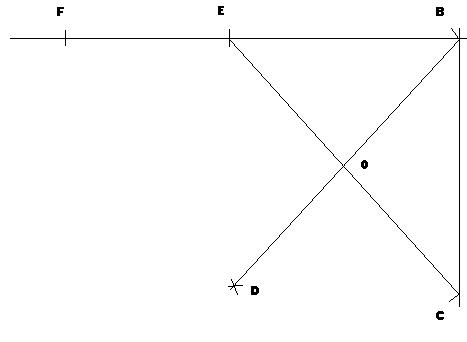
Soit la figure ci-dessous.
Les angles AÎK et BÎK ont le même sommet I et un côté commun [IK]. Ces angles sont appelés angles adjacents.
Construction des angles
Construction d'un angle de mesure donnée
Exercice:
Construire un angle dont la mesure est 25,5°
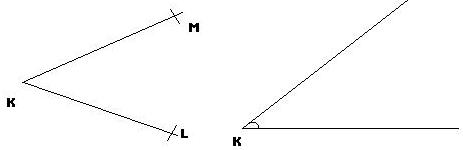
Reproduction d'un angle donnée
Nous pouvons reproduire un angle donné à l'aide d'un compas.
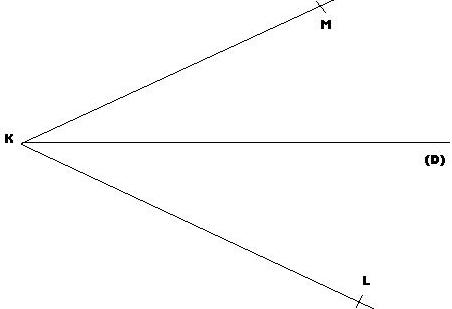
La bissectrice d'un angle est la droite passant le sommet de cet angle et qui divise cet angle en deux angles de même mesure.
Dans un triangle la somme de toute les mesures des angles est égale à 180°.
Angles supplémentaires - angles complémentaires
Angles supplémentaires
Des angles sont supplémentaires lorsque la somme de leur mesure est égale à 180°.
Angles complémentaires
Des angles sont complémentaires si la somme de leur mesure est égale à 90°.
Angles opposés par sommet
Activité
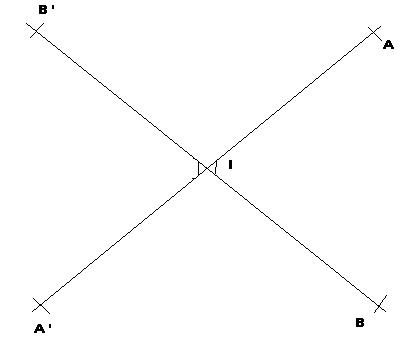
Construisons la symétrie de l'angle BÎA par rapport au point I.
Deux angles sont opposés par le sommet si les côtés de l'un sont des demi-droites aux côtés de l'autre.
Mesures des angles opposés par le sommet
Deux angles opposés par le sommet ont la même mesure
Angles formés par deux droites et une sécante
Présentation
Angle formés par deux droites parallèles et une sécante
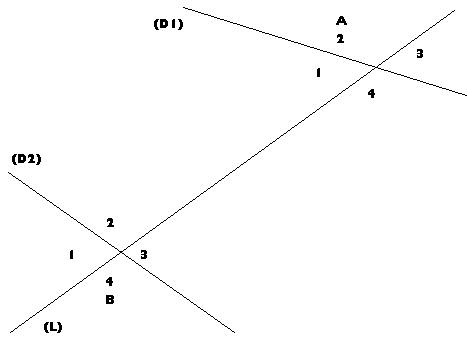
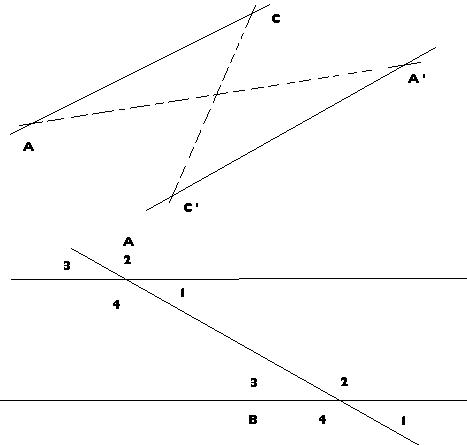
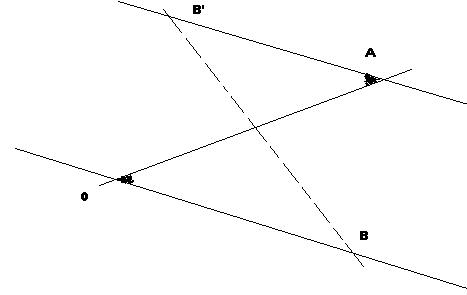
Construisons la symétrie de l'angle CÂI par rapport au point I. Cette figure fait apparaître 2 angles alternes internes.
Les angles alternes internes sont: Â1 et B3; Â4 et B2, A et B sont symétriques par rapport au point I (D1) et (D2) sont symétriques par rapport au point I, l'angle Â1 et l'angle B3 sont symétriques par rapport au point I alors mesÂ1 = mesB3, car 2 symétrie par rapport à un point ont même mesure. Si 2 angles alternes internes sont formés par 2 droites parallèles et une sécante, alors ils ont une même mesure. Si deux angles correspondant sont formés par 2 droites et une sécante, alors ils ont même mesure.
Justifié que deux droites sont parallèles
Avec deux angles alternes internes
Propriété
Si deux droites forment avec une sécante deux angles alternes internes de même mesure alors ces deux droites sont parallèles.
Avec deux angles correspondants
Si deux droites forment avec une sécante deux angles correspondantes de même mesure, alors ces droites sont parallèles
Angles d'un triangle
Somme des mesures des angles d'un triangle
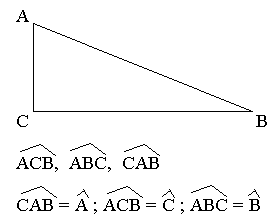
mesB + mesC + mes = 180°
Dans tout triangle la somme des mesures de ces angles est égale à 180°
Construction d'un triangle connaissant des longueurs de côtés ou des mesures d'angle
Triangle connaissant les longueurs de deux côtés et la mesure d'un angle
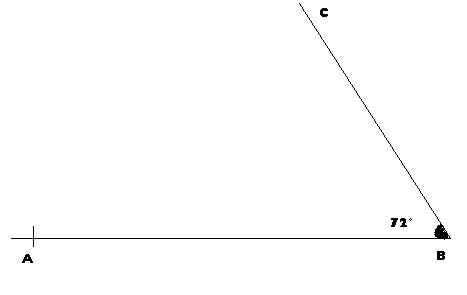
L'unité de longueur est le centimètre. Construisons un triangle ABC tel que AB = 5, BC = 6 et mes ABC = 72°
Deux triangles sont superposables s'ils ont un angle de même mesure compris entre deux côtés respectivement de même longueur.
Triangle connaissant la longueur d'un côté et les mesures de deux angles
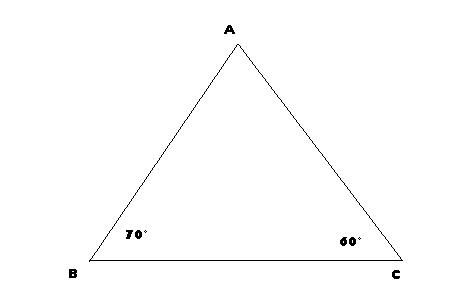
Construisons un triangle ABC tel que BC=5cm; mesB=70°, mesC=60°
Deux triangles sont superposés s'ils ont chacun un côté de même longueur, compris entre deux angle respectivement de même mesure
Triangle connaissant les longueurs des trois côtés
Construisons un triangle ABC tel que:
AB=3cm; AC=5cm et BC=6cm
Deux triangles sont superposés s'ils ont les trois côtés respectivement de même longueur.