Les symétries

Points symétriques par rapport à un point

Soit la droite.

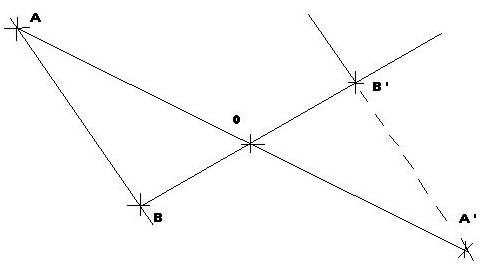
Nous constatons que O est le milieu du segment [AB], on dit alors que les points A et B sont symétriques par rapport à O.
Dire que A est symétrique de B par rapport à O signifie que AO=OB.

Construction du symétrique d'un point par rapport à un autre point donné

Exemple:

Construisons le symétrique de F' par rapport à I.

Nous pouvons réaliser une telle construction à l'aide d'un compas.

Propriété des symétriques par rapport à un point.

Droites symétriques

Activité:

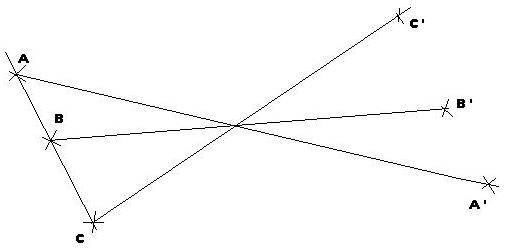
Le segment [AB] est l'image du segment du segment [A'C'] par rapport à O.

Propriétés:

Le segment [AC] est l'image du segment [AC] par rapport à O
Lorsque les points sont alignés leur symétrie par rapport é un point O sont aussi alignés. Si les points A et B ont pour symétrie par rapport au point O, les points A' et B' les droites (AB) et (A'B') sont aussi symétriques au points O.

Segments et angles symétriques

Activité:

Les segments [AB] et [A'B'] par rapport à O.
Propriété:
Deux segments symétriques par rapport à un point ont la même longueur. Deux angles symétriques par rapport à un point ont la même mesure: Â = Â'

• Précédent
• Suivant