Page 2 sur 4
Les symétries - Figures admettant un centre de symétrie
Index de l'article
Figures admettant un centre de symétrie
Activité:
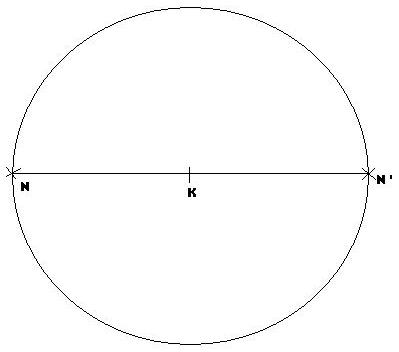
Traçons un cercle de centre K et marquons un point
Propriété:
Le centre d'un cercle est le centre de symétrie de ce cercle. Une symétrie est appelée centrale.
Symétrie orthogonale Construction du symétrie d'un point donné par rapport à une droite
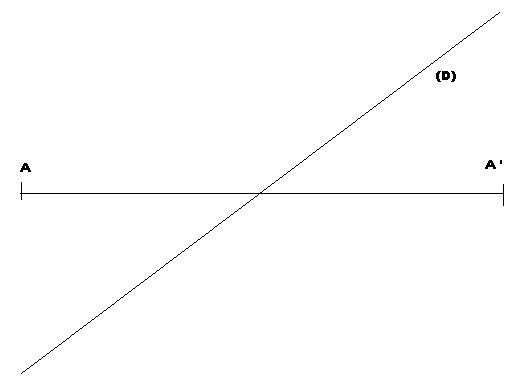
Soit la droite (D) ci-dessous.
Pour construire le symétrie d'un point par rapport à une droite, il faut que A (D) = (D) A
Propriétés des figures symétrie par rapport à une droite
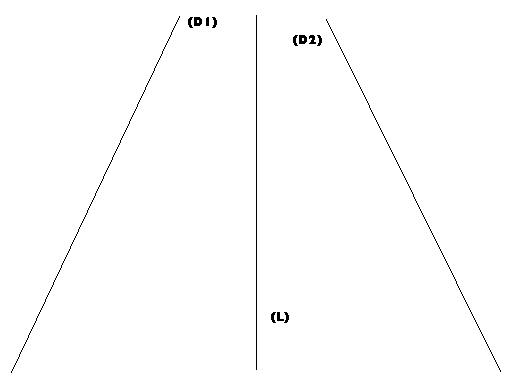
1ère Propriété: droites symétriques.
Lorsque les points sont alignés, leurs symétries par rapport à une droite (D) sont aussi alignées. Deux droites (D1) et (D2) symétrique par rapport à la droite (L) sont parallèle.
2ème Propriété: Segment et angles symétriques.
- Deux segments [AB] et [A'B'] symétriques par rapport à une droite ont la même longueur
- Deux angles symétriques par rapport à une droite ont la même mesure.
Figure admettant un axe de symétrie
Axe de symétrie:
La droite (D) passe par le milieu du carré (elle divise se carré en deux parties égales). Elle est donc appelée axe de symétrie.
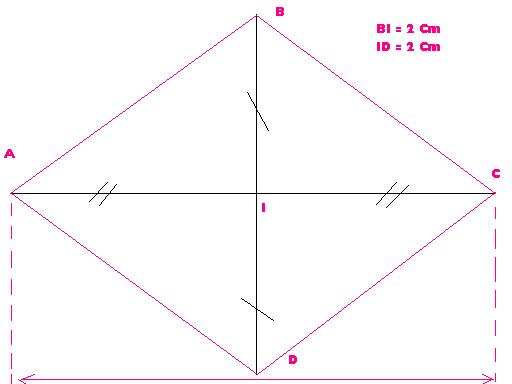
Le losange
Un losange est un quadrilatère dont les diagonales se coupent en un milieu et sont perpendiculaires.
- Un losange est un parallélogramme.
- Les côtés d'un losange ont la même longueur.
- Les diagonales d'un losange sont perpendiculaires mais n'ont pas la même longueur.
La surface d'un losange est: S = (h x l) / 2
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale