Les symétries - Utilisation des symétries pour démontrer

Utilisation des symétries pour démontrer

On donne le point O et trois points A, B et C non alignés. P, Q et R sont les images respectives de A, B et C par la symétrie de centre O.

Démontrez que les triangles ABC et PQR sont superposables

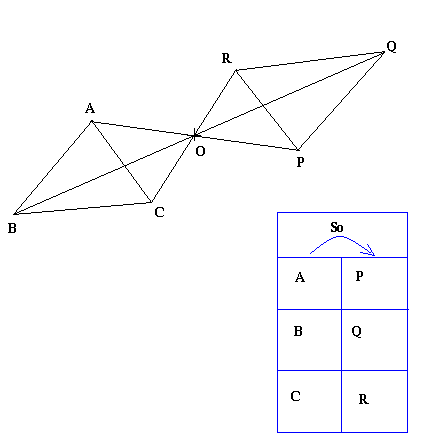
Exercice d'application 1:

On donne un cercle (C) de centre O et deux points E et F de (C), S_o est la symétrie de centre O. Complétez le tableau de correspondance et la figure ci-contre. Expliquez la méthode de construction des points E' et F'

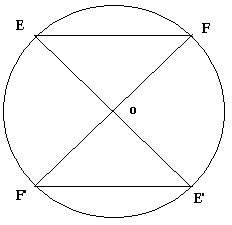
O est le centre du cercle (C) par conséquent il est le centre de symétrie du cercle (C), ce qui veut dire que tout point de (C) a pour symétrique par rapport à O un autre point de (C). Donc il suffit de construire ces diamètres ayant une extrémité, le point E ou le point F. Les symétrique de E et F par rapport à O seront chacun un point diamétralement opposé à F

Exercice d'application 2:

On donne cercle (C) de centre O, deux points E et F de (C) et un point P de (EF), S_o est la symétrie de centre O. Complétez le tableau de correspondance et la figure ci-contre.
Expliquez la méthode de construction P'

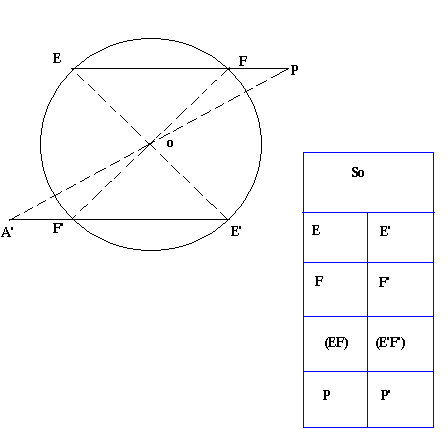
PE (EF) donc P, E et F sont alignés et nous savons que les symétriques de trois points alignés sont des points alignés.
Donc S_o(EF) = (E'F')
P', E' et F' sont des points alignés.

Exercice d'application 3:

ABCD est un rectangle, E l'image du point A par S_o et F l'image du point B par SC.

• Démontrez que (EF) est l'image de la droite (AB) par la symétrie orthogonale d'axe (DC) .
  Justifiez que ABFE est un rectangle
• Démontrez que le centre O de ce rectangle appartient à [DC]

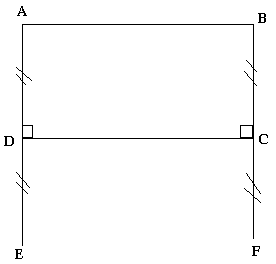
ABCD est un rectangle donc (AB) est perpendiculaire à (BC) et (AD) perpendiculaire à (BC)
S_DA=E signifie que c'est le milieu [AE].
(DC) est donc la médiatrice de [AE].