Un solide est en mouvement de rotation lorsque ses différents points décrivent des trajectoires circulaires par rapport à un repère donné.

---

Notion de moment d'inertie

La position de centre d'inertie ne suffit pas pour déterminer les caractéristiques de mouvement d'un solide soumis à l'action des forces acquis sous l'action d'une impulsion extérieure dépend de la distribution des masses à l'intérieur du solide.
Pour tenir compte de l'influence de ce dernier critère dans le mouvement de rotation d'un solide on introduit une nouvelle caractéristique: le moment d'inertie.
Le mouvement d'inertie d'un système par rapport à un axe est par définition la somme du produit des parties ponctuels i par le carré de la distance de cette partie à l'axe.

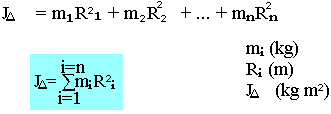
Exercice d'application 1

Soit à déterminer le mouvement de deux points matériel de masse respective m₁=4Kg et m₂=7Kg situer à 6Cm et à 2Cm de l'axe respectivement.
J = m₁R₁² + m₂R₂² = 4(6x10^-2)² + 7(2x10^-2)²
J = 1,75 x 10^-2 Kgm²

Exercice d'application 2

Déterminer le moment d'inertie d'un pendule simple de longueur 15Cm et de masse 3Kg
J = ml²
J = 3(15x10^-2)²
J = 6,75x10^-4 Kgm²

Théorème de Huygens

Le moment d'inertie d'un système de masse M par rapport à un axe de rotation quelconque est égal à son moment d'inertie par rapport à son centre d'inertie parallèle D augmenté du produit de la masse du système par le carré de la distance qui sépare les deux axes.
J_D = J_G + M.d²

Loi fondamentale de la dynamique

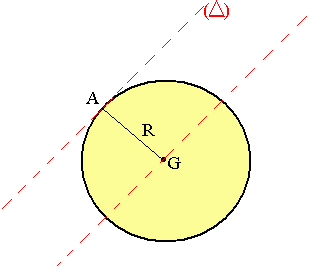
Soit à déterminer le moment d'inertie d'une circonférence de masse M de rayon R par rapport à un axe horizontal perpendiculaire au plan de la circonférence et passant par un point A de cette circonférence
J_D = J_G + Mr² or J_G = Mr²
J_D = Mr² + Mr²
J_D = 2Mr²

Remarque:

Pour un cerceau au circonférence pesant de masse M de rayon R. Pour un cylindre creux de masse M et de rayon R. Pour une poulie de masse M repartie sur sa circonférence de rayon R. J_G=M.R²

Pour un cylindre plan de masse M et de rayon R

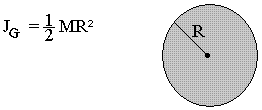
Pour un disque plein de masse M et de rayon R

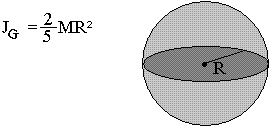
Pour un sphère pleine de rayon R de masse M

 

 

---

Loi fondamentale de la dynamique appliquée sur un solide en mouvement de rotation

Enoncé de la loi

Le produit du moment d'inertie d'un système en mouvement de rotation par rapport à un axe D par la variation temporelle de la vitesse angulaire est égale au moment de la force extérieure qui lui imprime ce mouvement

Exercice d'application

Soit à établir l'équation du mouvement d'un pendule pesant au tour d'axe fixe, et la distance neutre le centre de rotation et le centre d'inertie a

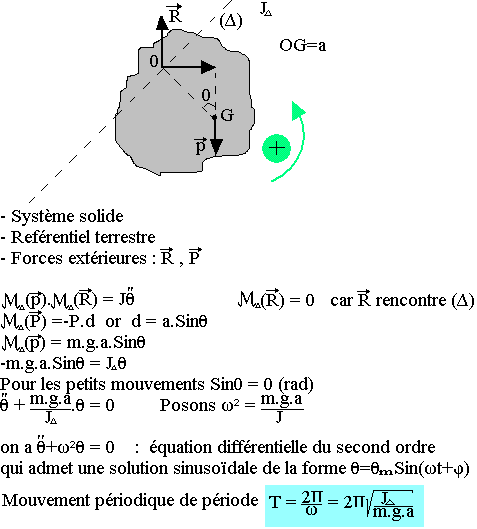
On appelle pendule pesant un solide susceptible d'effectuer des oscillations au tour d'un axe ne passant pas par son centre d'inertie. Dans le cas particulier du pendule simple le moment d'inertie est

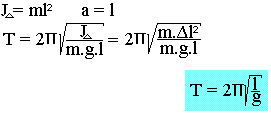
Remarque:

Dans la pratique on se retrouvera avec des systèmes effectuant à la fois un mouvement de translation et un mouvement de rotation. On divisera le système en sous système et appliquer pour chacun le principe ou la loi particulière.

 

---

Complément du cours: L'ENERGIE CINETIQUE

On définit l'énergie cinétique d'un système de masse m en, mouvement de translation à la vitesse V par : E_c=½m.v²

Pour un système de moment d'inertie J_D en mouvement de rotation uniforme à la vitesse O, on définie l'énergie cinétique par:

Théorème de l'énergie cinétique pour système en translation

La variation de l'énergie cinétique d'un point matériel ou d'un système en mouvement de translation entre deux instants est égale à la somme algébrique des travaux de toutes les forces extérieures qui s'appliquent au système entre ces deux instants:

Exercice d'application

On lance une bille de masse m vers le bas avec la vitesse V₀ à l'instant t=0, à t₁ cette bille arrive au sol avec une vitesse V₁.
Force appliquée: Poids:
W_(P) = P_AB = m.g.h

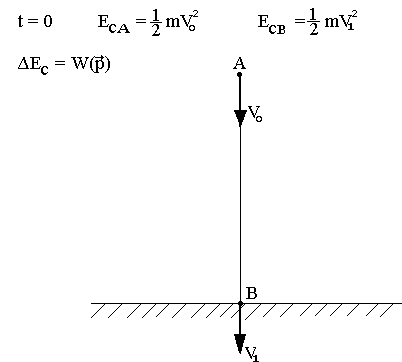
½m.V_B² - ½m.V_A² = m.g.h
V_B² - V_A² = 2g.h
V_B = (2g.h + V_A²)^½

Théorème de l'énergie cinétique pour un système en mouvement de rotation

La variation de l'énergie cinétique d'un point matériel ou d'un système de point matériel en mouvement de rotation entre deux instants est égal à la somme algébrique des travaux des moments des forces extérieures appliquées à ce point matériel entre ces deux instants:

Remarque:

Au cours d'un choc entre deux particules nous avons deux hypothèses:

Exercice

Un disque homogène de masse et de rayon R partant du repos roule sans glisser suivant la ligne de plus grande pente d'un plan incliné par rapport à l'horizontal.
Déterminer la nature du mouvement du disque.