Loi fondamentale de la dynamique appliquée sur un solide en mouvement de rotation

Enoncé de la loi

Le produit du moment d'inertie d'un système en mouvement de rotation par rapport à un axe D par la variation temporelle de la vitesse angulaire est égale au moment de la force extérieure qui lui imprime ce mouvement

Exercice d'application

Soit à établir l'équation du mouvement d'un pendule pesant au tour d'axe fixe, et la distance neutre le centre de rotation et le centre d'inertie a

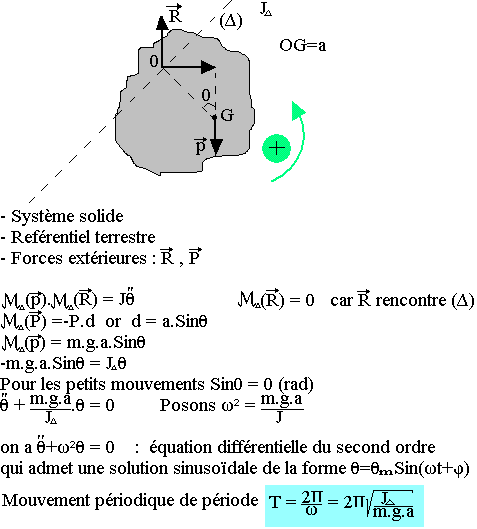
On appelle pendule pesant un solide susceptible d'effectuer des oscillations au tour d'un axe ne passant pas par son centre d'inertie. Dans le cas particulier du pendule simple le moment d'inertie est

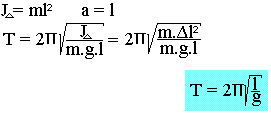
Remarque:

Dans la pratique on se retrouvera avec des systèmes effectuant à la fois un mouvement de translation et un mouvement de rotation. On divisera le système en sous système et appliquer pour chacun le principe ou la loi particulière.