Complément du cours: L'ENERGIE CINETIQUE

On définit l'énergie cinétique d'un système de masse m en, mouvement de translation à la vitesse V par : E_c=½m.v²

Pour un système de moment d'inertie J_D en mouvement de rotation uniforme à la vitesse O, on définie l'énergie cinétique par:

Théorème de l'énergie cinétique pour système en translation

La variation de l'énergie cinétique d'un point matériel ou d'un système en mouvement de translation entre deux instants est égale à la somme algébrique des travaux de toutes les forces extérieures qui s'appliquent au système entre ces deux instants:

Exercice d'application

On lance une bille de masse m vers le bas avec la vitesse V₀ à l'instant t=0, à t₁ cette bille arrive au sol avec une vitesse V₁.
Force appliquée: Poids:
W_(P) = P_AB = m.g.h

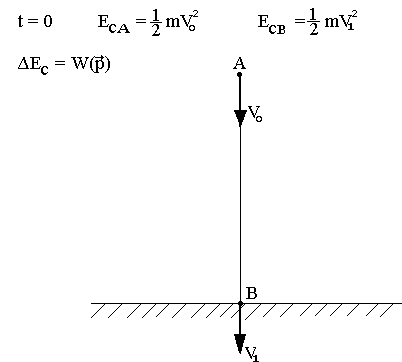
½m.V_B² - ½m.V_A² = m.g.h
V_B² - V_A² = 2g.h
V_B = (2g.h + V_A²)^½

Théorème de l'énergie cinétique pour un système en mouvement de rotation

La variation de l'énergie cinétique d'un point matériel ou d'un système de point matériel en mouvement de rotation entre deux instants est égal à la somme algébrique des travaux des moments des forces extérieures appliquées à ce point matériel entre ces deux instants:

Remarque:

Au cours d'un choc entre deux particules nous avons deux hypothèses:

• Soit le choc est dit mou ce qui a pour conséquence la non conservation de l'énergie cinétique
• Soit le choc est élastique: il y'a conservation de l'énergie cinétique c'est-à-dire l'énergie cinétique avant le choc est égale au choc après le choc.
• Lorsqu'un système effectue un mouvement mixte: rotation et translation, la variation de l'énergie cinétique du système est égale à la somme algébrique de tous les travaux des forces extérieures et des moments des forces extérieures appliquées au système:

Exercice

Un disque homogène de masse et de rayon R partant du repos roule sans glisser suivant la ligne de plus grande pente d'un plan incliné par rapport à l'horizontal.
Déterminer la nature du mouvement du disque.