Vibration et signaux

Phénomène périodique

Un mouvement est dit périodique lorsqu'il se répète identique à lui-même pendant des intervalles de temps successifs et égaux appelés période. Si le phénomène est rapide, il est appelé mouvement vibratoire et caractérisé par sa fréquence: T=1/f.
Période et fréquence sont deux entités inverses.
Un mouvement vibratoire est dit sinusoïdal lorsque l'élongation d'un point vibratoire est une fonction sinusoïdale de temps:
x = x_mCos(ωt+Þ)
y = y_mSin(ωt+Þ)
x et y: élongation
x_m et y_m amplitude max ou élongation
ω: la pulsation
Þ: phase à l'origine.
Pour les commodités de travail, on représentera une équivalence à un mouvement vibratoire par un vecteur tournant donc les caractéristiques sont les suivantes:

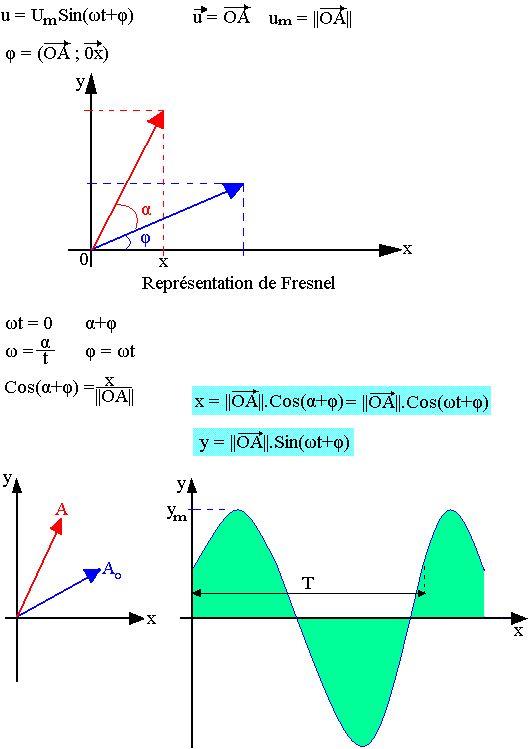
Le vecteur U=OA effectue un mouvement de rotation uniforme au tour du point O à la vitesse angulaire constante ω.

Remarque et application

u₁ = u_1mSin(ωt+Þ₁) et u₂ = u_2mSin(ωt+Þ₂).
D'après le théorème de Fourrier il existe une fonction u=u₁+u₂ u=u_mSin(ωt+Þ) en posant u=u_mSinωt il suffit pour déterminer u de trouver u_m et Þ

Application numérique

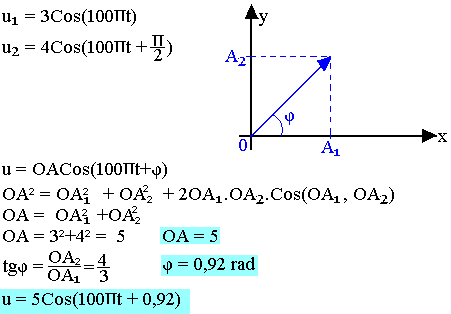
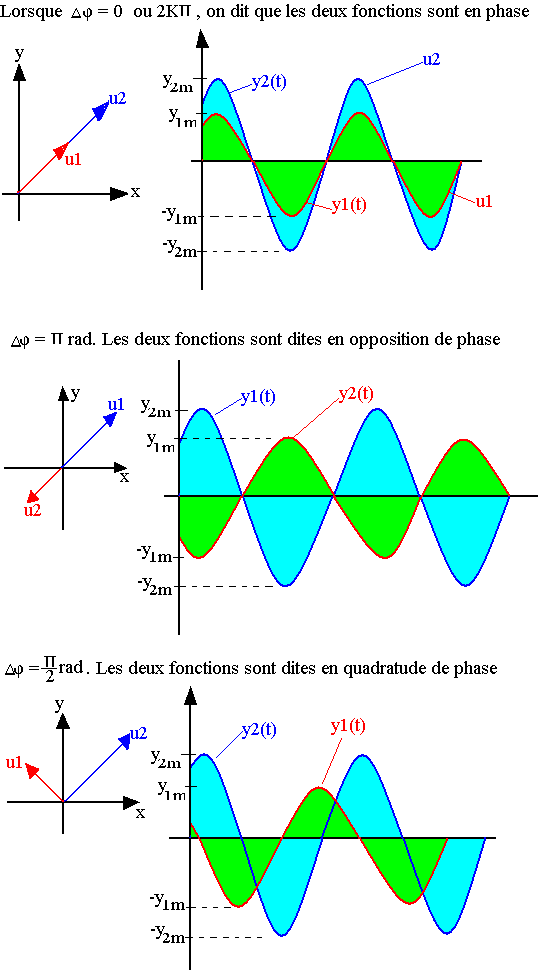
90° est supérieur à +. On dit que la fonction u₂ est en avance de phase par rapport à la fonction u₁.
On appelle déphasage entre deux fonctions d'onde u₁ et u₂ de phase initiale respective Þ₁ et Þ₂, la grandeur DÞ=Þ₂-Þ₁