Phénomène périodique

Un mouvement est dit périodique lorsqu'il se répète identique à lui-même pendant des intervalles de temps successifs et égaux appelés période. Si le phénomène est rapide, il est appelé mouvement vibratoire et caractérisé par sa fréquence: T=1/f.
Période et fréquence sont deux entités inverses.
Un mouvement vibratoire est dit sinusoïdal lorsque l'élongation d'un point vibratoire est une fonction sinusoïdale de temps:
x = x_mCos(ωt+Þ)
y = y_mSin(ωt+Þ)
x et y: élongation
x_m et y_m amplitude max ou élongation
ω: la pulsation
Þ: phase à l'origine.
Pour les commodités de travail, on représentera une équivalence à un mouvement vibratoire par un vecteur tournant donc les caractéristiques sont les suivantes:

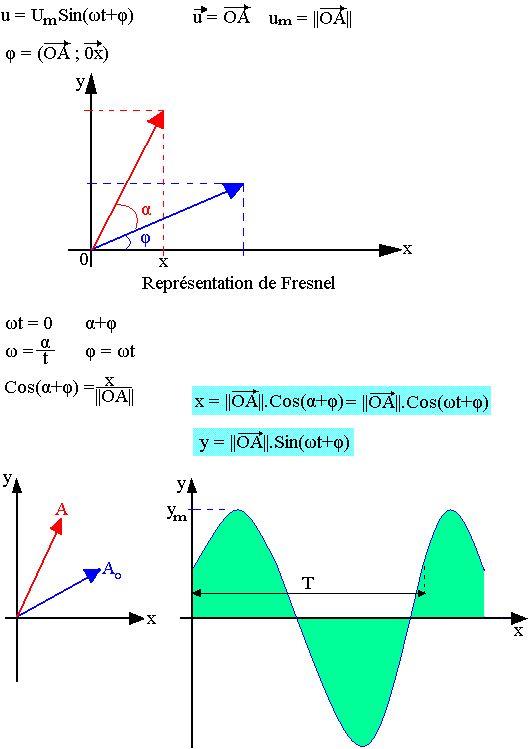
Le vecteur U=OA effectue un mouvement de rotation uniforme au tour du point O à la vitesse angulaire constante ω.

Remarque et application

u₁ = u_1mSin(ωt+Þ₁) et u₂ = u_2mSin(ωt+Þ₂).
D'après le théorème de Fourrier il existe une fonction u=u₁+u₂ u=u_mSin(ωt+Þ) en posant u=u_mSinωt il suffit pour déterminer u de trouver u_m et Þ

Application numérique

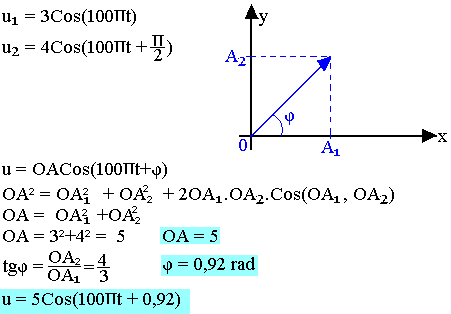
90° est supérieur à +. On dit que la fonction u₂ est en avance de phase par rapport à la fonction u₁.
On appelle déphasage entre deux fonctions d'onde u₁ et u₂ de phase initiale respective Þ₁ et Þ₂, la grandeur DÞ=Þ₂-Þ₁

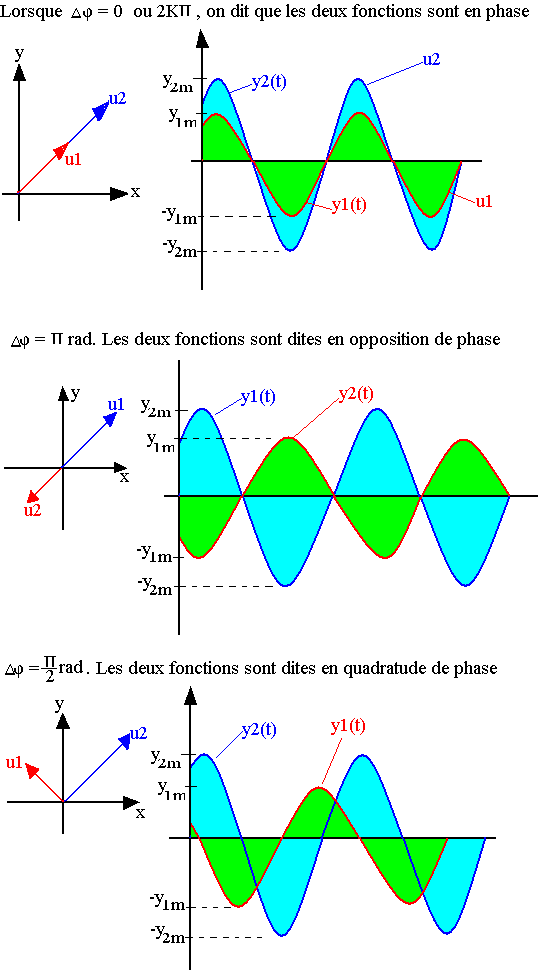
Etude expérimentale des mouvements vibratoires: la stroboscopie

La stroboscopie, un procédé pour l'étude des mouvements vibratoires. Elle consiste à ralentir ou à immobiliser le phénomène de façon apparente.

Principe

Pour observer un mouvement périodique de période T on éclaire le dispositif par une suite d'illumination très brève de période T_e ou T'. On substitue ainsi un mouvement réel, un mouvement apparent donc les caractéristiques dépendent de T et T_e

Montage et condition d'observation

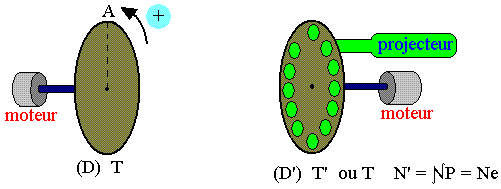
Si N est la vitesse de rotation du disque et P le nombre de trou, alors la fréquence des éclaires est B'=N_P.
La fréquence des éclaires doit être au moins égale à 20Hz et leur durée assez brève (environ le 100^e de la période du mouvement à étudier). Grâce à la persistance des impressions lumineuses sur la rétine, l'expérimentateur a l'illusion d'une observation continue.

L'immobilisation apparente

Supposons T=T_e, la période du disque (D) est égale à la période de T_e des éclaires, le rayon OA apparaît toujours à la même position et paraît donc immobile. Il en est de même si la période T_e est un multiple de celle du disque: T_e=k.T ; N_e=N/k
En effet le rayon OA est éclairé N fois tous les k tours et sur le fond noir du disque il y'a immobilité apparente de l'unique rayon OA.
Par contre su T=k.T_e alors N=N_e/k; le rayon OA est éclairé k fois par tour et sur le fond noir du disque il apparaît toujours en immobilité apparente une étoile blanche à k branches.

Ralenti apparent

Le rayon tournant OA étant éclairé dans la position OA, le prochain éclaire se produit après un instant T_e, légèrement supérieur et légèrement inférieur à I.

T_e légèrement supérieur à T

Le disque (D) aura effectuée un peut plus d'un tour et apparaîtra en OA₁. L'éclaire suivant le surprendra en OA₂ et ainsi de suite.

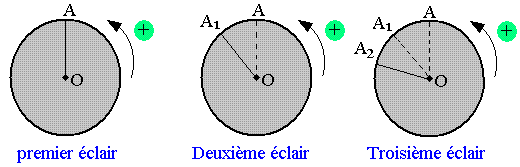
L'impression de l'observateur est celle d'un mouvement continu dans le sens réel de rotation: On parle de ralenti direct.

T_e légèrement inférieur à T

Entre deux éclaires consécutifs le disque (D) n'a pas effectué une rotation complète et le rayon OA est surpris dans les positions OA, OA'₁, OA'₂

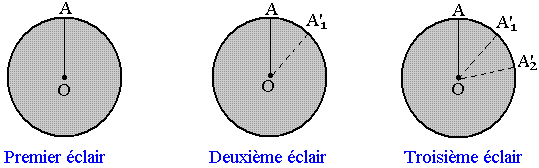
L'impression de l'observateur est celle d'un mouvement ralenti dans le sens contraire de rotation réel du disque: On parle de ralenti dans le sens rétrograde ou ralenti indirect.

Calcul de la fréquence du mouvement apparent ralenti

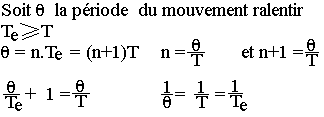
N_a = N - N_e
N_a: fréquence du mouvement apparent ralenti
N: fréquence du mouvement réel
N_e: fréquence des éclaires
N_a > 0 : mouvement apparent sens direct
N_a < 0 : mouvement apparent sens rétrograde.