Onde progressive
Si on laisse tomber une goutte d'eau à la surface libre d'un liquide au repos, on observe qu'il naît au point de chute des rides circulaires qui s'agrandissent progressivement en s'éloignant de ce point ceci est dû à la propagation dans toutes les directions à la surface du liquide de la déformation créée au point de chute. La cause de la perturbation est appelée émetteur. La déformation qui se propage s'appelle onde progressive. Le point où la perturbation est créée s'appelle la source. L'environnement qui permet la propagation de l'onde est le milieu de propagation: Dans un milieu homogène une onde se propage à lui même vitesse et dans toutes les directions est la vitesse de propagation est donnée par la relation v=d/t.
La période T est la période posée à la source par l'émetteur.
L'équation ou l'élongation de la source est de la forme Ys=aSin(ωt+Þ)
On appelle longueur d'onde la distance parcourue par l'onde pendant une période de mouvement de la source.
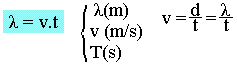
Lorsqu'une onde se propage dans la direction de la perturbation, elle est dite longitudinale. Et si elle se déplace dans une direction perpendiculaire à celle de la perturbation, elle est dite transversale.
Equation de l'onde en un point M du milieu de propagation
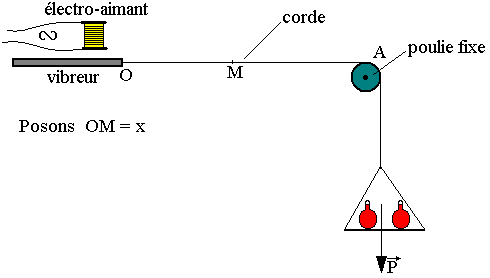
Considérons une corde fixée en O à un vibreur et passant par A par la gorge d'une poulie de masse négligeable. Cette corde est tendue à l'aide des masses marquées fixées de l’autre côté de la poulie.
Le mouvement transversale appliqué à la source a pour équation Y0=aSin(ωt+Þ). Le point M reproduit le mouvement de la source O.
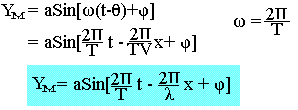
D'après cette équation l'onde en M vibre avec un double périodicité temporale T et spatial.
On montre que l'ébranlement créé en O se propage le long de la corde avec une vitesse ou une célérité.
v = c = (F/µ)½
F(N): tension de la corde
µ(Kg/m): masse linéaire (ou linéique) de la corde.
Pour deux points M1 d'abscisse OM1=x1 et M2 d'abscisse OM2=x2 en posant
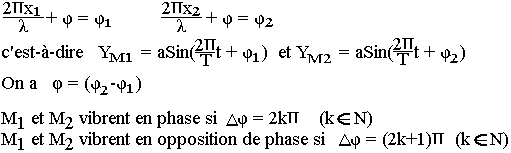
Remarque:
La célérité du son est donnée par la relation:

