Les ondes stationnaires

On appelle ondes stationnaire le résultat de la superposition de deux ondes progressives synchrones se propageant dans la même direction mais en sens contraire mais en sens contraire dans le même milieu de propagation.

La corde de MELDE

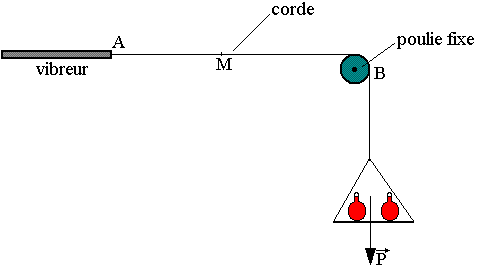
La corde de MELDE est une corde AB donc les extrémités B et A sont respectivement fixes et actionnées par vibreur de fréquence déterminée. La perturbation imprimée en A à la corde initialement au repos se propage le long de celle-ci; elle se réfléchit en B et rebrousse chemin. La corde est le siège des ondes l'une incidente et l'autre réfléchie. En tout point M de la corde et à tout instant la perturbation se propage à la vitesse C= (F/µ)^½
En éclairage stroboscopique normale on observe sur la corde des fuseaux donc les renflements sont appelés ventre et les extrémités noeuds

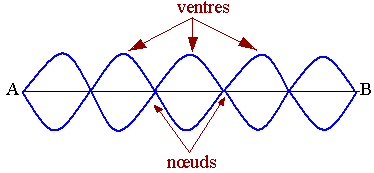
En éclairage stroboscopique la corde présente l'aspect d'une sinusoïde dont l'amplitude varie progressivement. La sinusoïde n'avance pas mais se déforme sur place d'où le nom d'onde stationnaire.

Analyse mathématique

Pour les commodités de travail, on considère le point B comme l'origine du repère

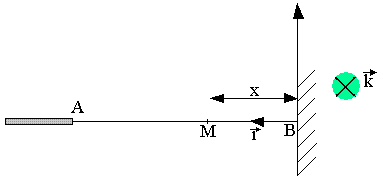
L'onde incidente qui arrive en B a pour équation y_IB=aSinωt, l'onde réfléchie qui part de B est y_RB telle que
Y_IB+Y_RB = 0
Pour le point M l'onde incidente y arrive avant d'atteindre l'origine.

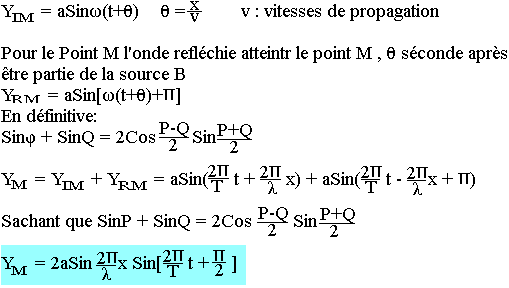
Le point M appartient à un noeud de vibration si son amplitude est nulle

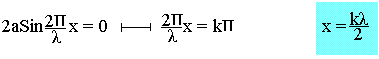
On montre que la distance entre deux noeuds consécutifs est

M appartient à un ventre de vibration si son élongation est maximale

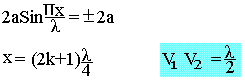
Si x_A-x_B=l (longueur de la corde)
Si A et B sont les noeuds de vibration

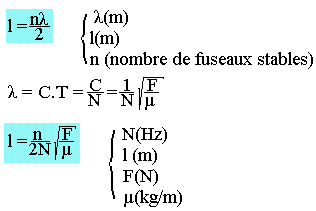
On montre également qu'on peut obtenir des ondes stationnaires sur onde AB donc l'extrémité B est libre ou mobile. L'expression de la longueur de la corde est

n (nombre de fuseaux stables)