Le champ électrique et le potentiel
Notion de champ électrique
Soit une charge q placée en un point O, d'après la loi de Coulomb, l'espace qui entoure cette charge possède la propriété d'exercer une force électrique sur toute charge qu'on y introduit. On peut donc définir en tout point de cet espace une force électrique. Cette espace constitue pour une charge Q un champ de force électrique ou plue brièvement un champ électrique E.
Pour reconnaître l'existence d'un champ électrique, il suffit d'observer si une charge Q est soumise à une force électrique Q est appelée charge test. On pose par définition
![]()
L'unité du champ électrique par définition est le N/C dans le système international on l'exprime en volt par mètre (V/m)
Expression du champ électrique
Cas d'une charge ponctuelle
Soit au point O une charge q et au point M la charge test Q. Pour déterminer le champ électrique au point M, il suffit de calculer la force agissante sur la charge Q et d'utiliser la définition du champ électrique E.
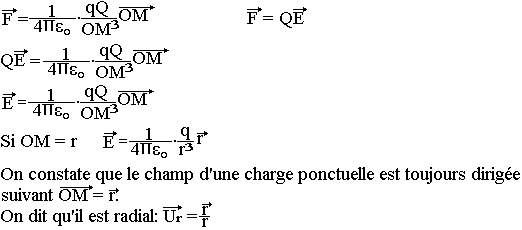
Cas d'une distribution de charge
Soit un ensemble de charge ponctuelle q1, q2, ..., qi placé aux points A1, A2, ... Ai, cherchons le champ électrique créé en un point M par cette distribution.
On détermine le champ créé au point M par chaque charge de la distribution et on fait la somme des champs obtenus.
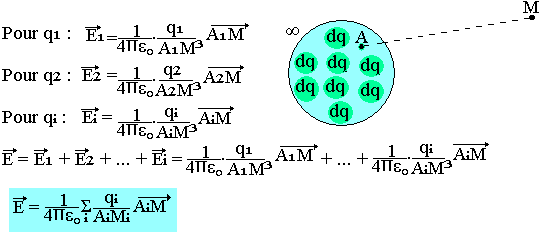
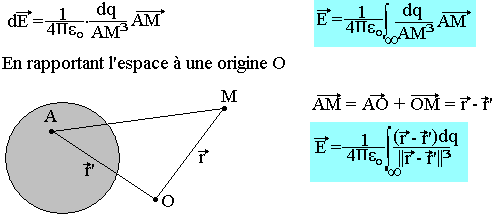
Dans le cas d'une distribution de charge continue, on peut toujours décomposer le domaine de la distribution en élément suffisamment petit pour être assimilé à des charges ponctuelle. Le champ électrique créé en un point M par l'élément du domaine délimité au tour d'un point A.
Remarque 1: Le champ électrique étant un vecteur, il est commode de déterminer ses composantes par projection des relations ci-dessus sur les axes convenables. Introduisons les axes (ox, oy, oz)
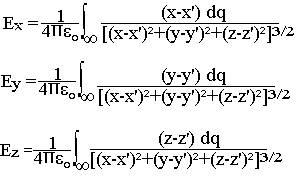
Remarque 2: Les propriétés de symétrie d'une distribution lorsqu’elles existent permettent de déterminer par avance la direction du champ électrique créé par la distribution.
Considérons une distribution qui possède un axe de symétrie et cherchons le champ électrique créé par cette distribution en un point M de l'axe de symétrie.
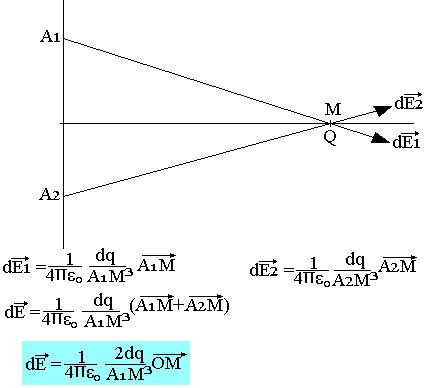
On peut décomposer la distribution en élément symétrique comme ci-dessus. Le choc créé par chaque couple est parallèle à OM, donc dirigé suivant l'axe de symétrie.
Lorsqu'une distribution de charge possède un axe de symétrie le champ électrique créé par toute la distribution en un point de l'axe de symétrie est dirigé suivant cet axe.
Circulation du champ électrique
Soit une charge q placée en O, cette charge crée au point M un champ électrique
![]()
Calculons la circulation de E lorsqu'on passe de M à M'
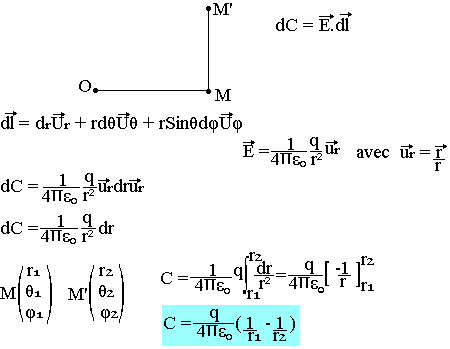
Cette circulation ne dépend pas du chemin suivi, le champ électrique dérive alors d'un potentiel. On doit avoir dC=-dU. On note habituellement V le potentiel électrique. Pour une charge ponctuelle:
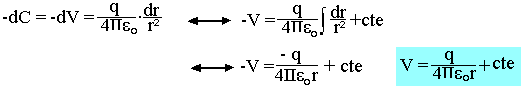
La constante dépend du choix d'origine des potentiels lorsque toutes les charges sont à distance finie. On admet que le potentiel est nul à l'infini.
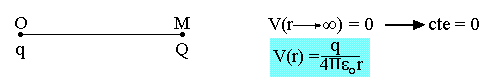
Soit les charges q1, q2, ..., qi, placées aux points respectifs A1, A2, ..., Ai. Le potentiel créé par q1 au point M est:
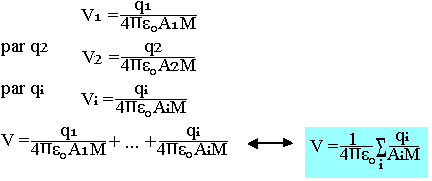
Dans le cas d'une distribution de charge continue, on calcule d'abord le potentiel créé en un point M par les éléments de la distribution.
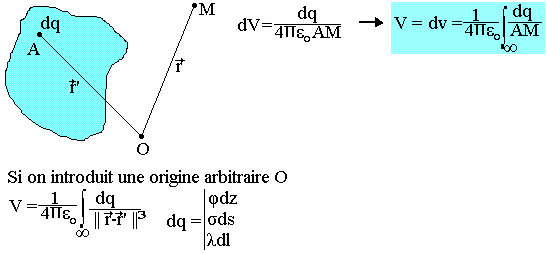
Flux du champ électrique
Flux du champ électrique créé par une charge ponctuelle à travers une surface S
Soit une charge ponctuelle Q, placée au point O et une surface (S) donnée. Soit M un point de S et ds l'élément de surface délimité au tour de M
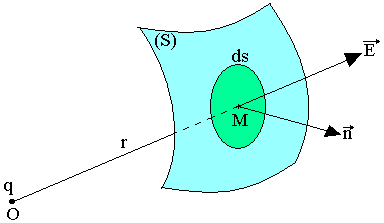
La charge q créée au point M le champ électrique
![]()
Et le flux du champ à travers la surface est:
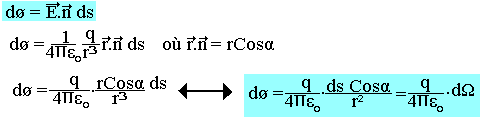
Pour déterminer le flux total on a:
![]()
Cas d'une distribution de charge ponctuelle à travers une surface (S)
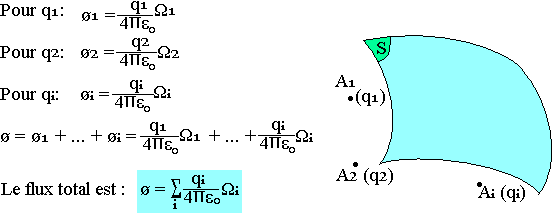
Le théorème de GAUSS
Dans le cas d'une surface fermée le résultat ci-dessus conduit à un théorème très utile dans la pratique: C'est le théorème de GAUSS.
Considérons un système de charge ponctuelle q1, q2, ..., qi placé aux ponts respectifs A1, A2, ... Ai et une surface fermée (S)
Certaines des charges sont peut être situées à l'intérieur de la surface. Ce sont des charges intérieures. D'autres peut être à l'extérieur et d'autres éventuellement à la surface. Le flux envoyé par ce système charge à travers la surface fermée considérée est:
Ø = flux des charges intérieures + flux des charges extérieurs + flux des charges à la surface
![]()
- Angle sous lequel d'un point intérieur à une surface on voit cette surface.
On rappelle que l'angle solide a pour mesure la surface intersectée sur la sphère des rayons unités par le cône donc la génératrice s'appuie sur le contour de la surface considérée.
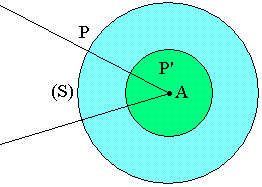
Soit P un point de la surface fermée donnée et P' l'intersection de (A(S)) avec la sphère de rayon unité. Lorsque P parcours la surface extérieure, P' décrit la sphère de rayon 1. Il s'en suit que l'angle solide sous lequel A intérieur on voit la surface fermée est:
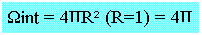
- Angle solide sur lequel d'un point situé à l'intérieur d'un solide de surface fermée, on voit cette surface.
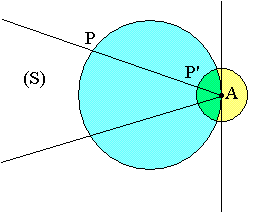
Lorsque P décrit la surface fermée, P' décrit la forme de sphère comprise entre la surface fermée et la tangente en A à la partie intérieure à la partie intérieure à cette surface. La surface décrite d'une demi sphère est:

- Angle solide sur lequel d'un point situé à l'extérieur d'un solide de surface fermée, on voit cette surface.
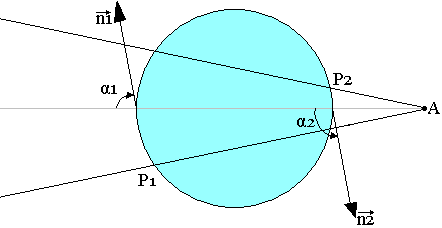
Un cône de sommet A d'angle au sommet découpe en général deux éléments de surface dS1 et dS2 sur la surface fermée donnée. Les angles solides correspondant à ces deux surfaces ont même valeur absolue mais de signe contraire.
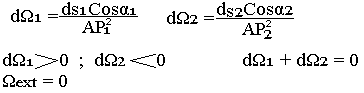
Le flux envoyé par le système de charge à travers une surface fermée est:

D'où le théorème appelé: théorème de GAUSS.
