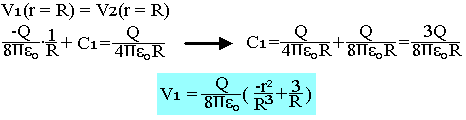Généralités
Pour calculer le champ électrique créé par une distribution continue de charge, on peut:
- Soit appliquer la définition
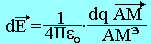
- Soit calculer V(r) dont on déduit
- Soit on utilise le théorème de GAUSS lorsqu'on connaît l'origine de E.
Dipôle électrique
On appelle dipôle électrique un ensemble de deux charges ponctuelle -q et +q placées à très petite distance l'une de l'autre.
Calcul du potentiel V
Soient les charges -q et +q placées respectivement aux points A et B cherchant le potentiel créé par ce système en un point très éloigné des deux charges.
Champ électrique créé par un dipôle
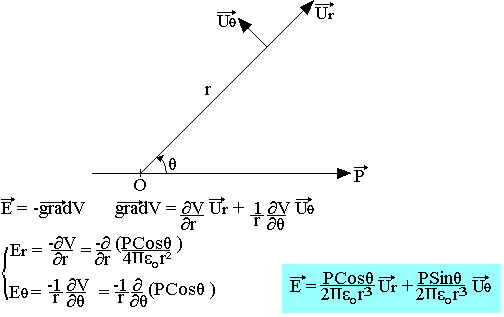
Approximation dipolaire d'une distribution quelconque de charge ponctuelle
Il s'agit de montrer que le potentiel créé par une distribution quelconque de charge ponctuelle dont la somme algébrique est nulle et est en premier approximation identique créé à celui d'un dipôle.
Considérons une distribution quelconque de charges ponctuelles situées près de l'origine et intéressons-nous au potentiel créé par cette distribution en un point M très éloigné de l'origine.
Par hypothèse si a est la grande distance séparant deux charges de la distribution, la distance de M à O est grand devant A.
Le potentiel créé par la distribution au point M alors:
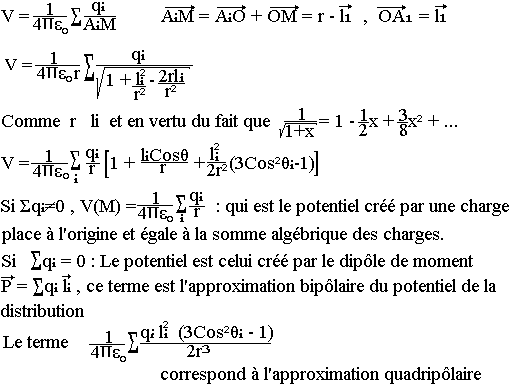
Fil rectiligne indéfini uniformément électrisé
Calcul du champ
Soit à calculer le champ électrique et le potentiel créé en un point M par un fil rectiligne de très grande longueur uniforme électrisé.
Soit O le pied de la perpendiculaire abaisser de M sur le fil.
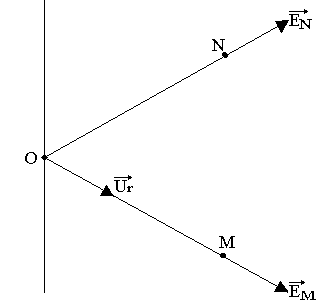
OM est un axe de symétrique donc le champ en M est dirigé suivant EM, il en est de même qu'au point N situé à la même distance du fil que M. Il en est ainsi pour tous les points situés sur la surface latérale du cylindre admettant le fil pour axe et de rayon r=OM
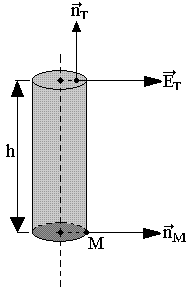
Cherchons le flux du champ électrique créé par le fil à travers la surface fermée définie par l'un de ces cylindres de hauteur h.
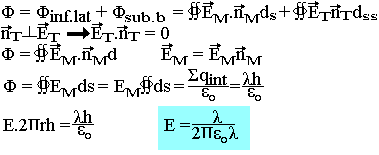
Calcul du potentiel
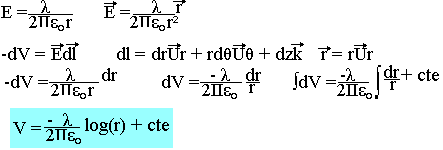
Disque circulaire uniformément chargé
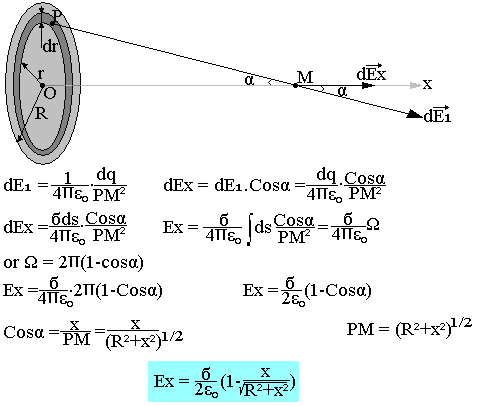
Soit à calculer le champ et potentiel en un point de l'axe d'un disque circulaire portant une densité de charge surfacique constante.
Calcul du champ
OM est un axe de symétrique donc le champ au point M est dirigé suivant OM. On cherche la projection sur OM du champ créé en M par la surface élémentaire comprise entre les cercles de rayon r et r+dr
Calcul du potentiel
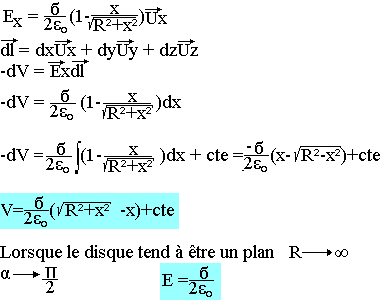
Sphère uniformément électrisée
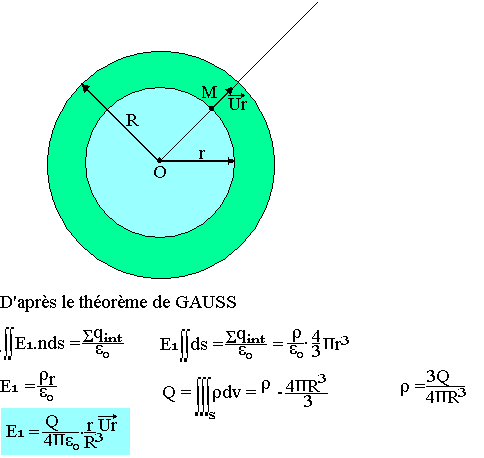
On se propose d'étudier le champ et le potentiel créé par un volume sphérique portant une densité de charge Þ uniforme (densité de charge volumique).
Soit O le centre de la sphère et M le point où l'on veut déterminer le champ électrique OM est axe de symétrique de la distribution (OM est un diamètre de la sphère). Donc le champ électrique au point M est dirigé suivant OM, le champ est radial. Le centre O de la sphère et le point M étant M ne modifie pas le problème électrique (on garde la même sphère et le même point M).
Calcul du champ
On choisit pour la surface de GAUSS une sphère centrée sur l'origine O, en tout point de cette surface, le champ est radial et son intensité est la même en tout point de la surface.
- Cas d'un point intérieur (r<R):
- Cas d'un point extérieur (r>R).
D'après le théorème de GAUSS:
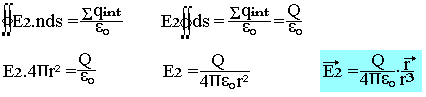
Calcul du potentiel
- Cas d'un point intérieur:
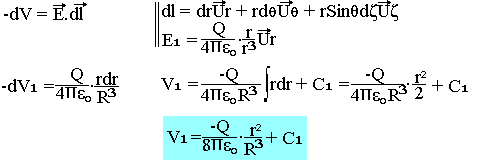
- Cas d'un point extérieur:
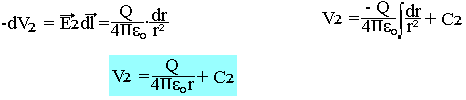
Comme il y'a pas de charge à l'infinie
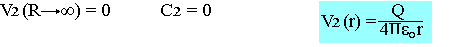
Il faut aussi qu'il y ait continuité des potentiels pour r=R. C'est donc en vertu de cela que V1(r=R)=V2(r=R)
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale