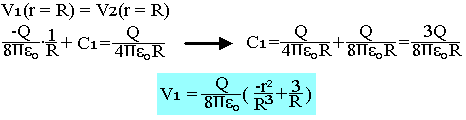Page 3 sur 3
Sphère uniformément électrisée
On se propose d'étudier le champ et le potentiel créé par un volume sphérique portant une densité de charge Þ uniforme (densité de charge volumique).
Soit O le centre de la sphère et M le point où l'on veut déterminer le champ électrique OM est axe de symétrique de la distribution (OM est un diamètre de la sphère). Donc le champ électrique au point M est dirigé suivant OM, le champ est radial. Le centre O de la sphère et le point M étant M ne modifie pas le problème électrique (on garde la même sphère et le même point M).
Calcul du champ
On choisit pour la surface de GAUSS une sphère centrée sur l'origine O, en tout point de cette surface, le champ est radial et son intensité est la même en tout point de la surface.
- Cas d'un point intérieur (r<R):
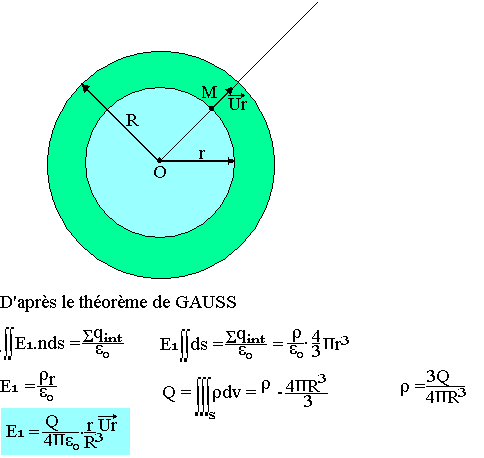
- Cas d'un point extérieur (r>R).
D'après le théorème de GAUSS:
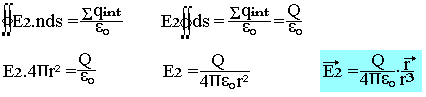
Calcul du potentiel
- Cas d'un point intérieur:
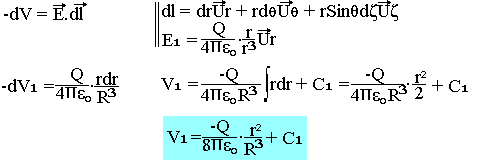
- Cas d'un point extérieur:
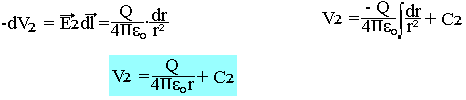
Comme il y'a pas de charge à l'infinie
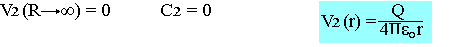
Il faut aussi qu'il y ait continuité des potentiels pour r=R. C'est donc en vertu de cela que V1(r=R)=V2(r=R)
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale