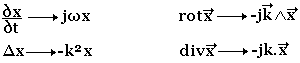---

Les ondes électromagnétiques planes

Etablissement des équations de propagation des champs E et B dans le vide.

Une onde électromagnétique est définie par deux champs E(M, t) et B(M, t) fonctions de 4 variables
t: variable temporelle
M: position de l'onde dans l'espace
Trois coordonnées spéciales et une temporelle. Une onde électromagnétique est qualifiée de plane lorsque ses coordonnées spéciales ne dépendent que d'un seul paramètre. On obtient alors deux champs E(x, t) et B(x, t) fonction d'une coordonnée spéciale et d'une coordonnée temporelle se propageant sur l'axe des x.
La solution générale des équations de propagation établit plis haut de la forme
E(x, t) = E₁(t-x/c) + E₂(t+x/c)
B(x, t) = B₁(t-x/c) + B₂(t+x/c)
où (E₁,B₁) et (E₂,B₂) sont deux champs électromagnétiques se propageant en sens inverse sur l'axe des x à la vitesse c.
Le champ (E₁(t-x/c) est une onde se propageant sans déformation le long de ox et dans me sens des x positifs : c'est une onde progressive.
E₂(t+x/c) est une onde se propageant sans déformation le long de ox dans le sens des x négatifs. La quantité t±x/c est la phase de l'onde à l'instant t.
A un instant t donné, la valeur de E₁ ou de E₂ est constante dans tout le plan x=constante: on dit que E₁ et E₂ décrivent une onde progressive plane (OPP). Dans le x négatif on dit que l'onde est répressive.

Vecteur de poynting et énergie électromagnétique

Le vecteur de poynting permet d'exprimer la puissance par mètre carré d'une onde électromagnétique.

Il décrit également la direction suivant laquelle s'écoule l'énergie électromagnétique et la densité volumique magnétique définies par:

Pour une onde progressive plane (OPP) le vecteur de poynting fonction de E et B et donné par les relations suivantes

Onde plane progressive harmonique

Une solution particulière de l'équation de propagation est l'onde dépendant sinusoïdalement du temps, est appelé onde plane progressive harmonique.
Pour une OPPH se propageant suivant (x, x') vers les x positifs, le champ électrique est de la forme:

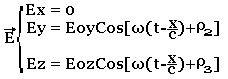
Où E_oy et E_oz sont les amplitudes et les phases φ₂ et φ₃ sont des constantes.

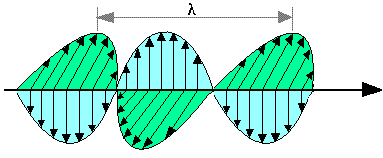
Pour Une OPPH, on définit les grandeurs suivantes:

Vitesse de phase, vitesse de groupe

Les différentes composantes du champ ci-dessous E et B font apparaitre

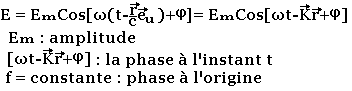
Les points tels que la phase wr-kr+φ est constante définissent à chaque instant t un plan perpendiculaire à la direction de propagation est appelée plan équiphase ou plan d'onde K est défini par:

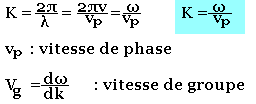
Dans le vide la vitesse de phase est constante Vφ=constante=c=3x10⁸m/s

Cas d'un milieu non dispersif

Ici la relation de dispersion (relation reliant w à k) est donnée par w=ck/n
n: étant l'indice de réfraction du milieu.
La vitesse de phase est alors constante et la relation équivalente est:

Cas d'un milieu dispersif

Ici l'indice de réfraction dépend de la pulsation w de l'onde. La relation de dispersion s'écrit alors:

 

---

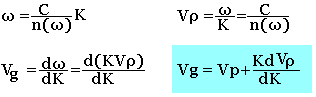
Onde électromagnétique dans un diélectrique (isolant)

Un diélectrique est une substance isolante capable d'emmagasiner de l'énergie. Il est caractérisé par sa permittivité de l'excitation électrique ou déplacement électrique et de l'intensité du champ électrique.
Pour un matériau donné la permittivité relative est normalisée par la permittivité du vide:

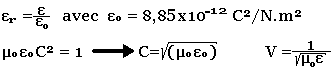
Dans le diélectrique la vitesse de propagation égale:
Où n est l'indice de réfraction.

 

---

Notion d'onde complexe d'une OPPH

Si on associe à toute composante réelle E ou B du champ la quantité complexe E est donnée par:

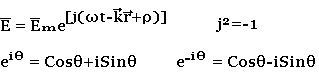
Les opérateurs différentielles se ramènent en cordonnées cartésiennes aux transformations algébriques suivantes: