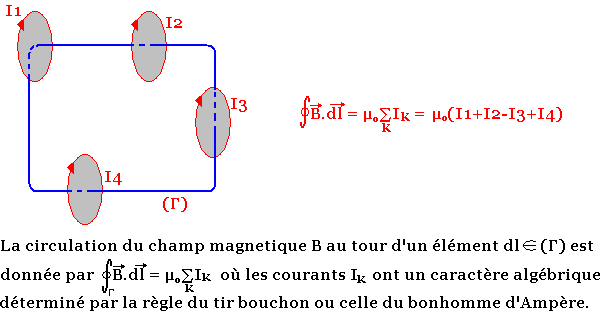
Généralités

Si l'électrostatique était le régime où la position des charges étaient indépendantes dans le temps, la magnétostatique est le régime où les champs et inductions magnétiques ne dépendent pas du temps
Les équations de la magnétostatique se réduisent à:

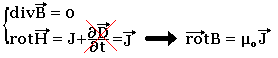
Force de LAPLACE: loi de BIOT et SAVART

Expérience

Soient deux conducteurs C₁ et C₂ parcourus respectivement par des courants I₁ et I₂ et situés à la distance d l'un de l'autre. Sur un élément dl du conducteur 2 s'exerce une force df₁ de même sur l'élément dl₁ s'exerce une force df₂ du au conducteur 1.

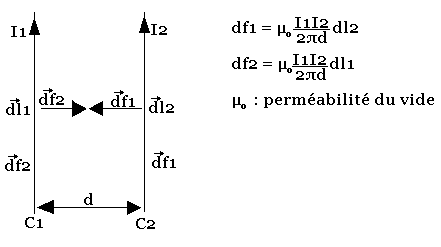
Les fils s'attirent si les courants sont de même sens et se repoussent dans le cas contraire.

Valeur de µ₀:

Etant donné expérimentalement 2 fils infinis distant de 14m, parcourus par des intensités de 1A et naissent entre eux sur des portions de 1m des forces d'égale valeur de 2x10^-7N. Déduire la valeur de µ₀ qui est la perméabilité du vide.

Force magnétiques dites de LAPLACE

Un circuit électrique C₁ créé en tout point de l'espace, un champ d'induction magnétique B₁ tel que sur un élément dl₂ sur un circuit C₂ parcouru par un courant I₂ s'exerce une force

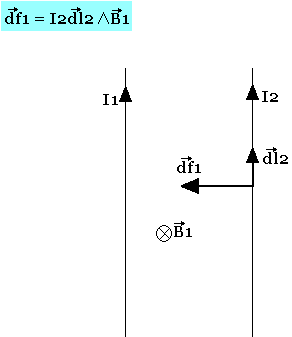
Ce résultat est connu sous le nom de force de LAPLACE.
Dans le cas d'une particule de charge q animée d'une vitesse V dans un champ B, la force de LAPLACE s'écrit:

Loi de BIOT et SAVART

La loi de BIOT et SAVART donne l'expression du champ magnétique créé en tout point de l'espace par un circuit électrique filiforme parcouru par un courant I.

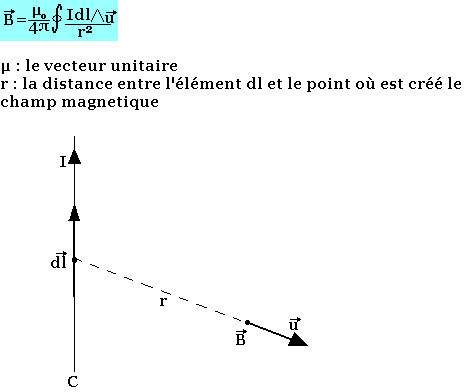
Pour une particule de charge Q animée d'une vitesse V, la loi de BIOT et SAVART s'écrit:

Pour des distributions volumiques ou surfaciques de courant la loi de BIOT et SAVART s'obtient en

Pour une répartition volumique et par

Pour une répartition surfacique.

Si dans un référentiel coexiste un champ électrique E, une induction magnétique E, une charge électrique q soumise à la superposition des forces électriques et magnétiques dites forces électrostatiques de LORENTZ d'expressions:

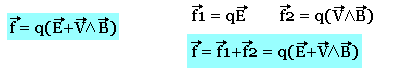
Les propriétés du champ magnétique

Le champ magnétique obéit aux propriétés suivantes::
La conservation du flux: Elle s'exprime sous la forme locale:

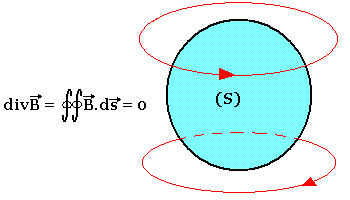
Le théorème d'Ampère