Généralités
Si l'électrostatique était le régime où la position des charges étaient indépendantes dans le temps, la magnétostatique est le régime où les champs et inductions magnétiques ne dépendent pas du temps
Les équations de la magnétostatique se réduisent à:
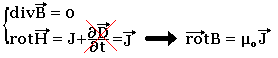
Force de LAPLACE: loi de BIOT et SAVART
Expérience
Soient deux conducteurs C1 et C2 parcourus respectivement par des courants I1 et I2 et situés à la distance d l'un de l'autre. Sur un élément dl du conducteur 2 s'exerce une force df1 de même sur l'élément dl1 s'exerce une force df2 du au conducteur 1.
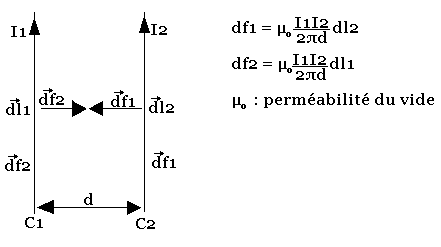
Les fils s'attirent si les courants sont de même sens et se repoussent dans le cas contraire.
Valeur de µ0:
Etant donné expérimentalement 2 fils infinis distant de 14m, parcourus par des intensités de 1A et naissent entre eux sur des portions de 1m des forces d'égale valeur de 2x10-7N. Déduire la valeur de µ0 qui est la perméabilité du vide.
Force magnétiques dites de LAPLACE
Un circuit électrique C1 créé en tout point de l'espace, un champ d'induction magnétique B1 tel que sur un élément dl2 sur un circuit C2 parcouru par un courant I2 s'exerce une force
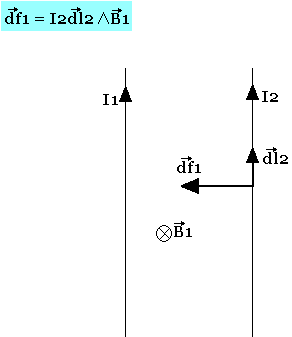
Ce résultat est connu sous le nom de force de LAPLACE.
Dans le cas d'une particule de charge q animée d'une vitesse V dans un champ B, la force de LAPLACE s'écrit:
![]()
Loi de BIOT et SAVART
La loi de BIOT et SAVART donne l'expression du champ magnétique créé en tout point de l'espace par un circuit électrique filiforme parcouru par un courant I.
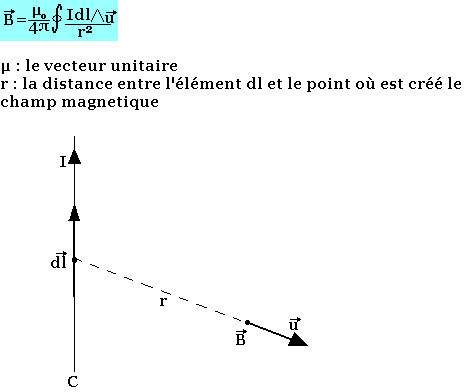
Pour une particule de charge Q animée d'une vitesse V, la loi de BIOT et SAVART s'écrit:
![]()
Pour des distributions volumiques ou surfaciques de courant la loi de BIOT et SAVART s'obtient en
![]()
Pour une répartition volumique et par
![]()
Pour une répartition surfacique.

Si dans un référentiel coexiste un champ électrique E, une induction magnétique E, une charge électrique q soumise à la superposition des forces électriques et magnétiques dites forces électrostatiques de LORENTZ d'expressions:
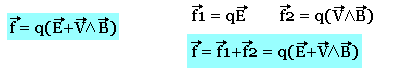
Les propriétés du champ magnétique
Le champ magnétique obéit aux propriétés suivantes::
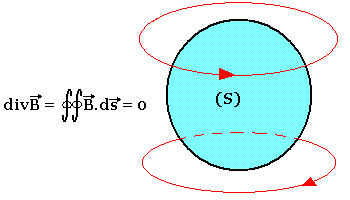
La conservation du flux: Elle s'exprime sous la forme locale:
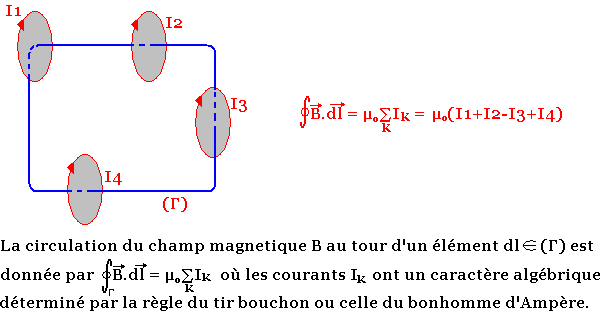
Le théorème d'Ampère
Potentiel vectoriel A: Relation de COLOMB
La relation
![]()
Entraîne l'existence d'un vecteur A appelé potentiel vecteur défini par la relation:
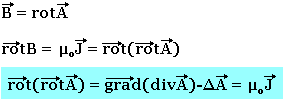
La Jauge de COLOMB consiste à chercher une solution A avec la condition supplémentaire
![]()
Ainsi le potentiel vectoriel obéit à l'équation aux dérivées partielles
![]()
Pour un circuit filiforme parcouru par un courant I, le potentiel vecteur s'écrit
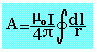
Energie potentielle
Soit un circuit (C) parcouru par un courant I et placé dans un champ magnétique B, ce conducteur est soumis à une force dite de LAPLACE donnée par
![]()
dl étant un élément de longueur pris sur (C)
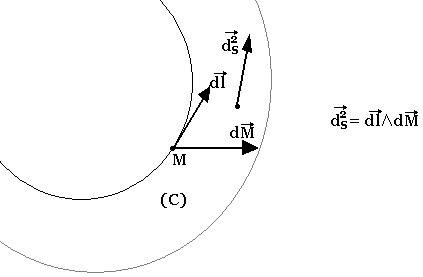
Pour un déplacement élémentaire dM d'un point du circuit, le travail de la force de LAPLACE s'écrit:
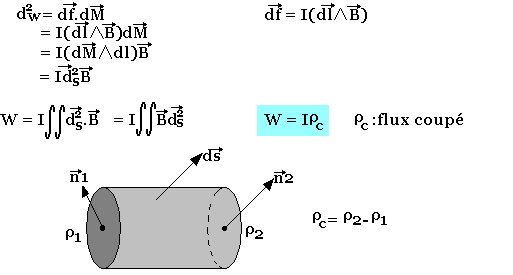
Ce travail ne dépend que de la position initiale et finale, il est assimilable à l'énergie magnétique Ep
Le phénomène d'induction
On considère deux circuits C1 alimentés par un générateur et C2 non alimenté mais possédant un galvanomètre G.
En éloignant ou en rapprochant C1 et C2 le galvanomètre détecte dans C2 un courant donc le sens est fonction du déplacement.
Dans les expériences où il y'a déplacement, le sens du courant est tel que la résultante de le force de LAPLACE nait de ce courant s'oppose au déplacement. Localement le champ au sens de variation du champ magnétique créé par le courant induit s'oppose au sens de variation du champ magnétique: ceci traduit la loi de LENZ. Les effets du courant induit s'opposent aux causes qui lui ont données naissance.
Le déplacement du circuit (2) fait apparaitre une force électrique induite
![]()
Où φc est le flux du champ magnétique à travers la surface engendrée par le déplacement de C2. Il est appelé flux coupé
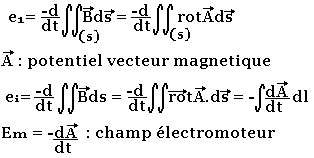
C'est ce champ électrique qui met en mouvement les porteurs mobiles soumis à la force de LAPLACE:
![]()
Les milieux magnétiques
Les dipôles magnétiques
On appelle dipôle magnétiques toute source de magnétisme quasi ponctuelle assimilable à une distribution localisée de courant donc les dimensions sont très petites devant les distances où s'exerce ses effets.
Pour un circuit filiforme C parcouru par un courant I, le mouvement magnétique M est donné par l'expression
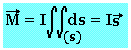
Où S est une surface quelconque s'appuyant sur le contour C et orienté suivant la règle du tire-bouchon.
Si P est un point quelconque du circuit S est donné par la relation
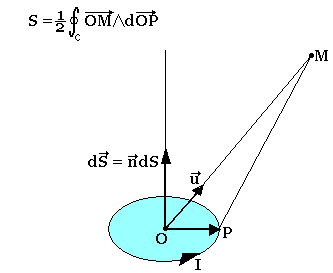
Le potentiel vecteur A en un point M distant du dipôle
![]()
Exercice
Sachant que B=rotA retrouvez l'expression du champ magnétique créé par le dipôle au point M (en coordonné sphérique)
