Potentiel vectoriel A: Relation de COLOMB

La relation

Entraîne l'existence d'un vecteur A appelé potentiel vecteur défini par la relation:

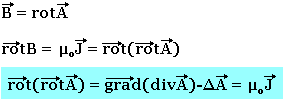
La Jauge de COLOMB consiste à chercher une solution A avec la condition supplémentaire

Ainsi le potentiel vectoriel obéit à l'équation aux dérivées partielles

Pour un circuit filiforme parcouru par un courant I, le potentiel vecteur s'écrit

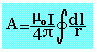
Energie potentielle

Soit un circuit (C) parcouru par un courant I et placé dans un champ magnétique B, ce conducteur est soumis à une force dite de LAPLACE donnée par

dl étant un élément de longueur pris sur (C)

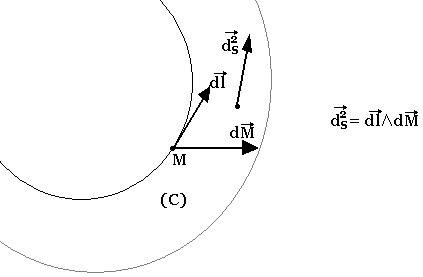
Pour un déplacement élémentaire dM d'un point du circuit, le travail de la force de LAPLACE s'écrit:

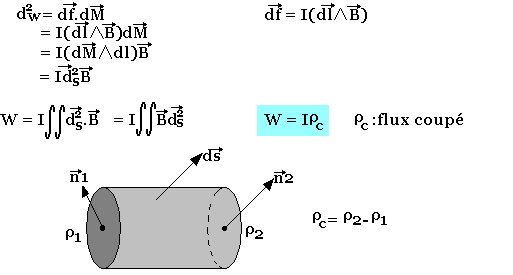
Ce travail ne dépend que de la position initiale et finale, il est assimilable à l'énergie magnétique E_p

Le phénomène d'induction

On considère deux circuits C₁ alimentés par un générateur et C₂ non alimenté mais possédant un galvanomètre G.
En éloignant ou en rapprochant C₁ et C₂ le galvanomètre détecte dans C₂ un courant donc le sens est fonction du déplacement.
Dans les expériences où il y'a déplacement, le sens du courant est tel que la résultante de le force de LAPLACE nait de ce courant s'oppose au déplacement. Localement le champ au sens de variation du champ magnétique créé par le courant induit s'oppose au sens de variation du champ magnétique: ceci traduit la loi de LENZ. Les effets du courant induit s'opposent aux causes qui lui ont données naissance.
Le déplacement du circuit (2) fait apparaitre une force électrique induite

Où φ_c est le flux du champ magnétique à travers la surface engendrée par le déplacement de C₂. Il est appelé flux coupé

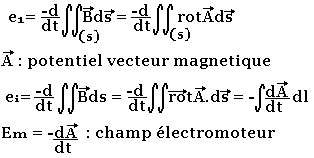
C'est ce champ électrique qui met en mouvement les porteurs mobiles soumis à la force de LAPLACE:

Les milieux magnétiques

Les dipôles magnétiques

On appelle dipôle magnétiques toute source de magnétisme quasi ponctuelle assimilable à une distribution localisée de courant donc les dimensions sont très petites devant les distances où s'exerce ses effets.
Pour un circuit filiforme C parcouru par un courant I, le mouvement magnétique M est donné par l'expression

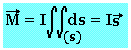
Où S est une surface quelconque s'appuyant sur le contour C et orienté suivant la règle du tire-bouchon.
Si P est un point quelconque du circuit S est donné par la relation

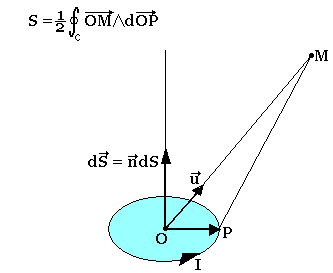
Le potentiel vecteur A en un point M distant du dipôle

Exercice

Sachant que B=rotA retrouvez l'expression du champ magnétique créé par le dipôle au point M (en coordonné sphérique)