Addition binaire
Opération d'addition
L'addition des nombres binaires se fait en respectant les règles suivantes:
- 0 + 0 = 0
- 0 + 1 = 1 + 0 = 1
- 1 + 1 = 10, On écrit "0" et on reporte "1" sur le bit de rang supérieur (rang de gauche)
- 1 + 1 + 1 = 11, on écrit "1" et on reporte "1" sur le bit de rang supérieur
Exemple:
Effectuons les opérations suivantes:
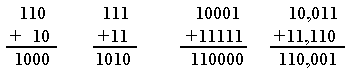
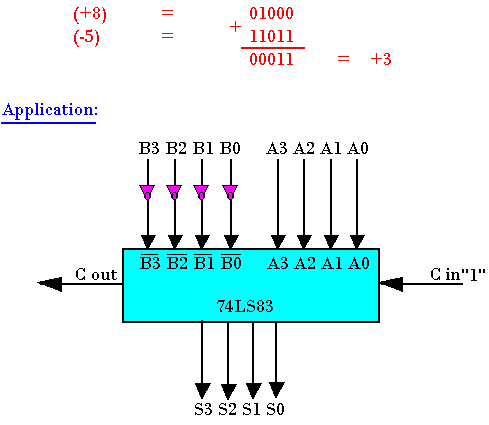
Conception d'un circuit additionneur
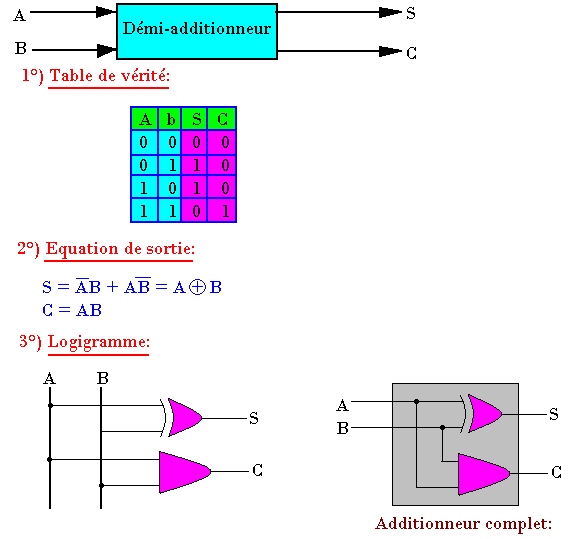
Le demi-additionneur
Il s'agit ici de concevoir un circuit capable d'effectuer la somme de deux nombres binaires a et b. Le circuit doit avoir deux entrées a et b, et deux sorties S et C
- S: Sortie du bit somme
- C: Carry (sortie du bit de report)
Additionneur complet
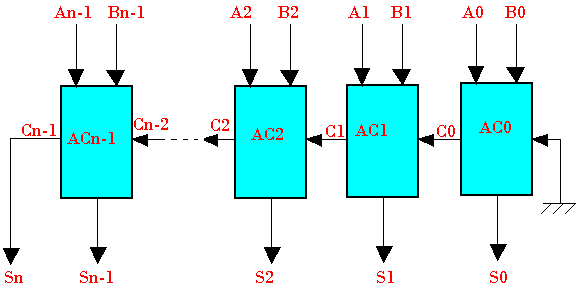
Un additionneur complet est un circuit capable de faire la somme de 3 bits An et Bn qui sont les bits à additionner et Cn-1 le report provenant de la somme des bits directement moins significatifs. Le circuit aura deux sorties Sn et Cn qui sont respectivement le bit de la somme et le bit du report provenant de la somme de 3 bits An, Bn et Cn-1.
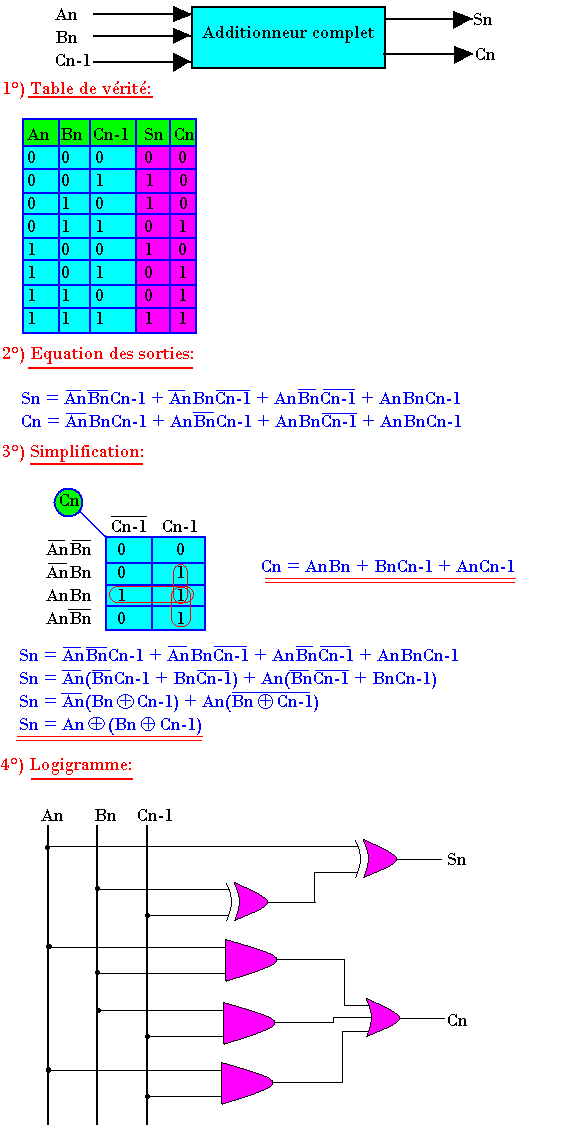
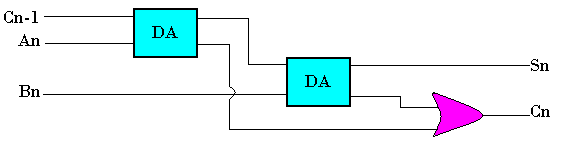
On peut réaliser un additionneur complet à partir de deux demis-additionneurs et d'une porte "OU"
Additionneur de deux nombres binaires de n bits
Soit à effectuer la somme de deux nombres N1 et N2:
- N1 est constitué de An-1 An-2… A2 A1 A0
- N2 est constitué de Bn-1 Bn-2 B2 B1 B0
A0 et B0 sont les LSB.
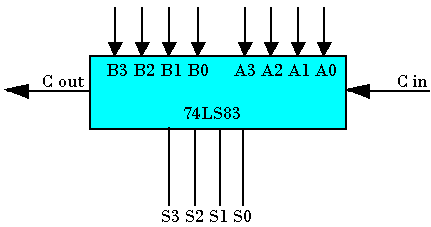
Additionneur 4 bits à CI (74LS83)
Soustraction binaire
Le complément à 1 d'un nombre binaire
Complémenter un nombre binaire à 1 consiste à changer tous les 0 et 1 et tous les 1 par les 0
Exemple: Le complément à 1 de
- 10111 est 01000
- 0101101 est 1010010
Le complément à 2 d'un nombre binaire
Le complément à 2 d'un nombre binaire revient à trouver son complément à 1 puis additionner 1 bit de rend 0 (le LSB)

Les nombres binaires signés
Jusqu'ici nous avons travaillés avec les nombres binaires notés en grandeur exacte. Or les nombres véhiculés dans la plus part des systèmes numériques (ordinateur) sont précédés par un bit de signe: par conversion "0" représente un nombre positif et "1" représente un nombre négatif.
- Pour représenter un nombre de n bits dans l'annotation "signe grandeur" ou notation "en complément à "2". On a besoin de (n+1) bits. Le (n+1)ième bit représente le bit de signe.
- Lorsqu'on représente un nombre négatif, le bit de signe est "1" et la valeur présentée est le complément à 2 de la grandeur exacte.
Exemple: Représenter les nombres décimaux suivants en notation signe grandeur ou notation en complément à 2.
+24 → (11000)2 = +24 = 011000
-24 → 24 = 11000
Le complément à 2 de 11000 est 01000
+13 → 13 = (1101)2 = +13 = 01101
-13 = 13 = (1101)2 = 10011
Changer le signe d'un nombre revient à complémenter à 2 ce nombre y compris le bit de signe
+45 = 0101101 son complément à 2 est 1010011 = -45
Les règles de la soustraction
- 0 - 0 = 0
- 0 - 1 = (on emprunte "1" ce qui fait 10-1, on écrit "1" et on retient 1)
- 1 - 0 = 1
- 1 - 1 = 0
- 0 - 1 - 1 = (on emprunte "1" ce qui fait 10-1-1, on écrit "0" et on retient "1")
- 1 - 1 - 1 = 0 - 1
Exemple d'application:
Effectuons les opérations de soustraction.
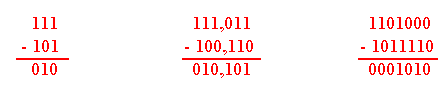
Addition de deux nombres positifs
+12 = 01100
+5 = 00101
Pour faire l'opération des nombres signés, ces nombres doivent avoir le même nombre de bit.
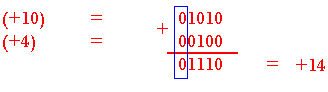
Addition d'un nombre positif et un nombre négatif plus petit en valeur absolue.
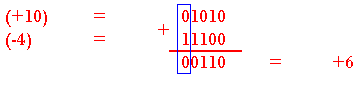
Addition d'un nombre positif et un nombre négatif plus grand en valeur absolue.
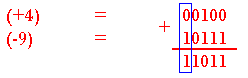
Le complément à 2 de 1011 est 0101 = 5
Le résultat 11011 = -5
Addition de deux nombres négatifs

Le complément à 2 de 0010 est 1110 = 14
Le résultat 10010 = -14
Addition de deux nombres égaux opposés
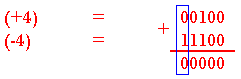
Le dépassement
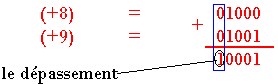
Lorsque la somme de deux nombres positifs donne un nombre négatif (bit de signe égal à 1) on dit qu'il y'a eu dépassement sur le rang de bit de signe. Le résultat obtenu est faux.
Soustraction par complément à 2
La soustraction par complément à 2 revient à complémenter le diminuanteur en suite additionner les deux nombres.
(diminuante + diminuanteur complémenté à 2)
Les deux nombres doivent avoir le même nombre de bits.
Exemple:
Effectuons l'opération (+8)-(+5).
Les nombres doivent être sur 5 bits y compris le bit de signe
(+8) = 01000
(+5) = 00101
Le complément à 2 de 00101 est 11011 = -5
Conception d'un soustracteur
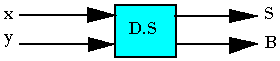
Le demi soustracteur
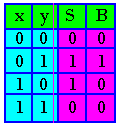
C'est un circuit capable de faire la soustraction de deux nombre binaires d'un bit chacun. Le circuit aura deux entrées x, y et deux sorties S et B
- S: Sortie du bit de soustraction
- B: Retenue (borrow)
a) Tableau de vérité:
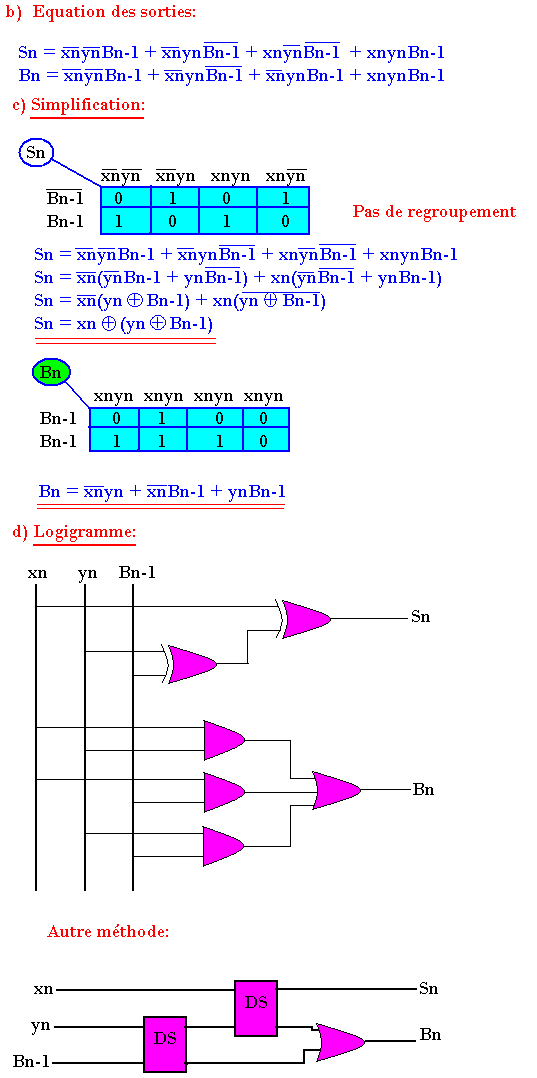
b) Equation des sorties:
![]()
Soustracteur complet
C'est un circuit capable de faire la soustraction de deux bits de rang n, (xn-yn) tout en tenant compte de la retenue Bn-1 provenant de la soustraction des bits de rang directement inférieurs. On aura deux sorties Sn et Bn.
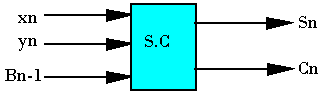
Table de vérité
|
xn |
yn |
Bn-1 |
Sn |
Bn |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
Multiplication binaire
Opération de multiplication
Les règles de calcul de la multiplication binaire sont pratiquement les mêmes qu'en décimal. Nous avons ainsi:
- 0 x 0 = 0
- 0 x 1 = 0
- 1 x 0 = 0
- 1 x 1 = 1
Application:
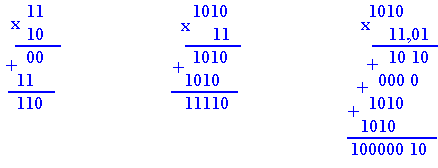
Lorsqu'une opération donne plus de deux produits partiels, effectuez la somme de ces derniers 2 à 2 pour diminuer le risque d'erreur.
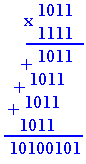
Conception d'un circuit multiplicateur
Exercice 1:
Conception d'un circuit multiplicateur de deux nombres d'un bit chacun.
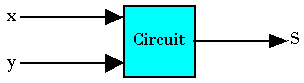
Tableau de vérité:
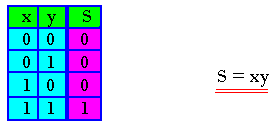
Logigramme:
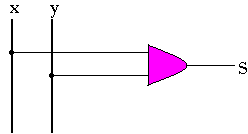
Division binaire
Même principe que la division des nombres décimaux xy
Exemple:

Exercice:
Conception d'un multiplicateur de deux nombres de 2 bits chacun: X(x1x0); Y(y1y0). La sortie sera un nombre binaire de 4 bits (S3S2S1S0)=Z.
S0, x0, y0 sont les LSB
S3, x1,y1 sont les MSB
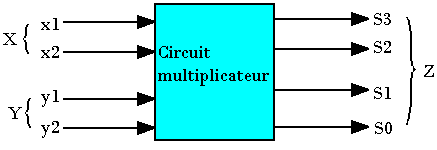
Travail à faire:
- Table de vérité
- Equation des sorties
- Logigramme
