Soustraction binaire
Le complément à 1 d'un nombre binaire
Complémenter un nombre binaire à 1 consiste à changer tous les 0 et 1 et tous les 1 par les 0
Exemple: Le complément à 1 de
- 10111 est 01000
- 0101101 est 1010010
Le complément à 2 d'un nombre binaire
Le complément à 2 d'un nombre binaire revient à trouver son complément à 1 puis additionner 1 bit de rend 0 (le LSB)

Les nombres binaires signés
Jusqu'ici nous avons travaillés avec les nombres binaires notés en grandeur exacte. Or les nombres véhiculés dans la plus part des systèmes numériques (ordinateur) sont précédés par un bit de signe: par conversion "0" représente un nombre positif et "1" représente un nombre négatif.
- Pour représenter un nombre de n bits dans l'annotation "signe grandeur" ou notation "en complément à "2". On a besoin de (n+1) bits. Le (n+1)ième bit représente le bit de signe.
- Lorsqu'on représente un nombre négatif, le bit de signe est "1" et la valeur présentée est le complément à 2 de la grandeur exacte.
Exemple: Représenter les nombres décimaux suivants en notation signe grandeur ou notation en complément à 2.
+24 → (11000)2 = +24 = 011000
-24 → 24 = 11000
Le complément à 2 de 11000 est 01000
+13 → 13 = (1101)2 = +13 = 01101
-13 = 13 = (1101)2 = 10011
Changer le signe d'un nombre revient à complémenter à 2 ce nombre y compris le bit de signe
+45 = 0101101 son complément à 2 est 1010011 = -45
Les règles de la soustraction
- 0 - 0 = 0
- 0 - 1 = (on emprunte "1" ce qui fait 10-1, on écrit "1" et on retient 1)
- 1 - 0 = 1
- 1 - 1 = 0
- 0 - 1 - 1 = (on emprunte "1" ce qui fait 10-1-1, on écrit "0" et on retient "1")
- 1 - 1 - 1 = 0 - 1
Exemple d'application:
Effectuons les opérations de soustraction.
Addition de deux nombres positifs
+12 = 01100
+5 = 00101
Pour faire l'opération des nombres signés, ces nombres doivent avoir le même nombre de bit.
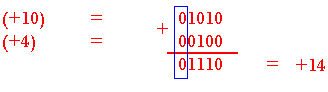
Addition d'un nombre positif et un nombre négatif plus petit en valeur absolue.
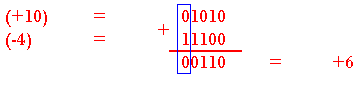
Addition d'un nombre positif et un nombre négatif plus grand en valeur absolue.
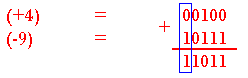
Le complément à 2 de 1011 est 0101 = 5
Le résultat 11011 = -5
Addition de deux nombres négatifs

Le complément à 2 de 0010 est 1110 = 14
Le résultat 10010 = -14
Addition de deux nombres égaux opposés
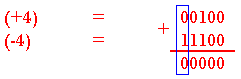
Le dépassement
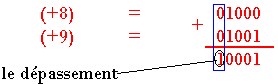
Lorsque la somme de deux nombres positifs donne un nombre négatif (bit de signe égal à 1) on dit qu'il y'a eu dépassement sur le rang de bit de signe. Le résultat obtenu est faux.
Soustraction par complément à 2
La soustraction par complément à 2 revient à complémenter le diminuanteur en suite additionner les deux nombres.
(diminuante + diminuanteur complémenté à 2)
Les deux nombres doivent avoir le même nombre de bits.
Exemple:
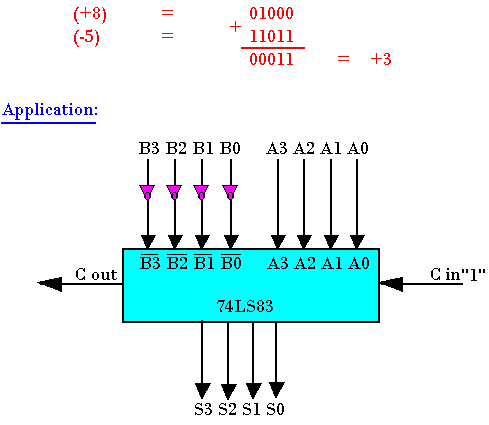
Effectuons l'opération (+8)-(+5).
Les nombres doivent être sur 5 bits y compris le bit de signe
(+8) = 01000
(+5) = 00101
Le complément à 2 de 00101 est 11011 = -5