Page 2 sur 5
Stabilité d'un système bouclé
Un système est stable si et seulement si la condition de BARKAUSIN est respectée. A savoir Tbo=T'=KH=-1. T tend vers l'infini
NB: On peut avoir une sortie non nulle pour une entrée nulle. De plus la condition KH=-1 est encore appelée condition de fonctionnement en oscillation, d'où
|KH|=1
Arg(KH)=-180°
Critère de stabilité
- Un système bouclé est instable si on a simultanément |KH| supérieur ou égal à 1 et Arg(KH)=180°
- Un système bouclé est stable si on a simultanément |KH|<1 et Arg(KH)=-180°
Exemple d'application
Dans un montage amplificateur les signaux de sortie prélevés en haute fréquence permettent d'avoir une transmitance:
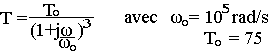
Cet amplificateur est inséré dans un système bouclé donc la fonction de transfert de la chaîne de réaction est un nombre réel positif K. On demande:
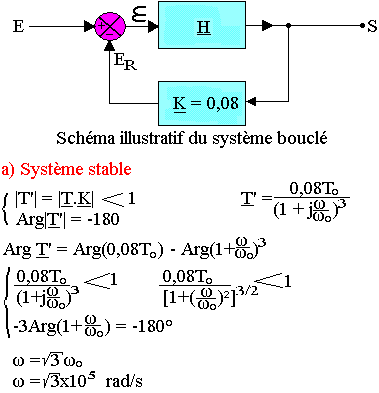
- Montrer que ce système est stable pour K=8%
- Pour qu'elles valeurs de K le système entre-t-il en oscillation
Donner un schéma illustratif du système bouclé.
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale