Modulation d'amplitude sur deux porteuses en quadrature (QAM : Quadrature Amplitude Modulation)

L'équation de la modulation QAM est une variante de celle du PSK. Dans la modulation PSK tous les points sont sur le cercle de valeur I et de Q, ont une relation entre eux avec les mêmes amplitudes. Si les amplitudes changent avec les symboles ainsi que la phase nous obtenons la modulation QAM.
Le QAM peut être considéré comme une combinaison de deux DSC-SC (Modulation à double bande latérale avec suppression de la porteuse).
L'équation du QAM peut être définie comme : X(t)=A_nCos(ωt+Ø_n) avec l'expression ou A_n et Ø_n
X(t)=A_n(tCos(ωt-B_n(t)Sinωt
A_n(t) = A_nCosØ_n
B_n(t) = B_nSinØ_n
Cette équation peut créer un mode hybride qui varie les amplitudes ainsi que les phases.

Exemple:

Prenons M=16 donc on a 16 symboles avec chaque symbole représentant le mot de 4 bits. Nous pouvons mettre ceux-ci sur le cercle mais elles seront très serrées donc le taux d'erreur va augmenter.

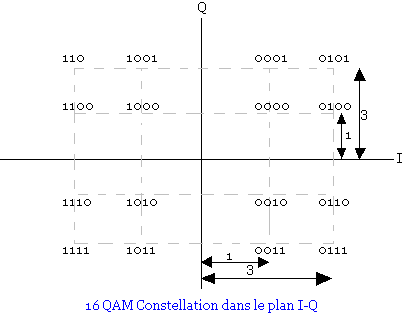
Dans la modulation QAM les points sont sur un rectangle contrairement PSK qui est sur le cercle.

Détection FSK

Le démodulateur FSK est réalisée à l'aide d'une boucle à verrouillage de phase PLL (Phase Look Loop)

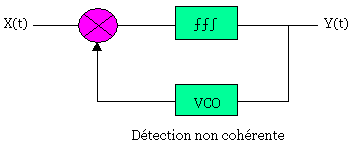
Le détecteur de phase mesure la différence de phase entre le signal de sortie de VCO et X(t). Une tension positive est produite si le signal X(t) est en avance de phase et une tension négative produite dans le cas contraire.

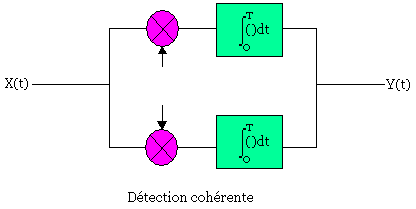
Détection

Cas de 2-PSK

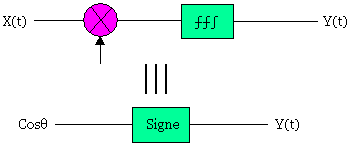
Toutes les décisions peuvent être basées sur le signe de Y, si Y est positif alors c'est le 1 logique où alors si Y est négatif c'est le 0 logique.

Cas de 4-PSK

X(t) = CosØCosωt
Y(Q)(t) = passe-bas (X(t)2Sinωt) = -SinØ
X(t) = -SinØSinωt
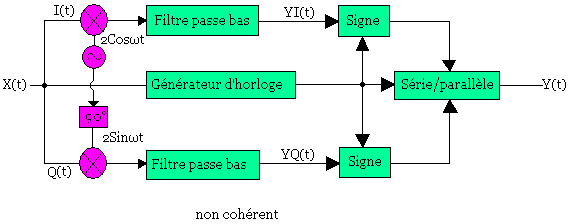
Y(I)(t) est la sortie du premier détecteur de phase tandis que Y(Q)(t) est la deuxième sortie du ,détecteur de phase. Tous les décisions peuvent être basées sur la polarisation de Y(I) et Y(Q).
On peut remarquer que si Y(Q) est positif alors la donnée D₁=1. Si Y(Q)(t) est négatif alors la donnée D₁=0
YQ(t)>0 → D₁="1"
YQ(t)<0 → D₁="0"
YI(t)>0 → D₀="1"
YQ(t)<0 → D₀="0"

Cas de 8-PSK

Deux méthodes sont possibles:

Première méthode: (4 détecteur de phase)

YI(t) = passe-bas[X(t)2Cosωt] = CosØ
YQ(t) = passe-bas[X(t)2Sinωt] = -SinØ
YA(t) = passe-bas[X(t)2Cos(ωt+0,707)] = 0,707(CosØ+SinØ)
YB(t) = passe-bas[X(t)2Sin(ωt+0,707)] = 0,707(CosØ-SinØ)

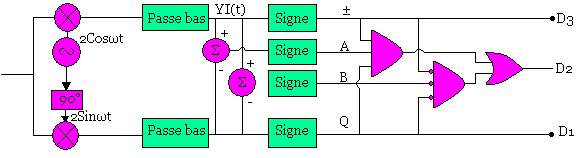
La méthode ci-dessus nous montre que les 3 bits de données sont déterminés de la manière suivante.
I(t)(signe):
YI(t)>0 → I="1"
YI(t)<0 → I="0"

Q(t)(signe)
YQ(t)>0 → Q="1"
YQ(t)<0 → Q="0"

A(t)(Signe)
YA(t)>0 → A="1"
YA(t)<0 → A="0"

B(t) (signe)
YB(t)>0 → B="1"
YB(t)<0 → B="0"

Deuxième méthode: (deux détecteurs de phase)

On remarque que YA et YB sont les combinaisons linéaires de YI et YQ.
YA(t) = 0,707YI(t)-0,707YQ(t)
YB(t) = 0,707YI(t)+0,707YQ(t)
Ainsi on n'a besoin que de deux détecteurs de phase.